Интегральная запись законов сохранения материи, количества движения и момента количества движения

Для ввода интегральных записей законов сохранения используют формулу (4.35)

1. Закон сохранения материи

Под интегральной характеристикой П будем понимать массу М, а под удельной величиной π – плотность ρ.

Согласно закону сохранения массы, материя не может возникнуть или исчезнуть. Это значит, что субстанциональная производная 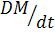должна быть равна нулю.

Т.е.

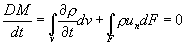(4.36)

это и есть математическая запись закона сохранения массы в интегральной форме.

Замечание:

Уравнение (4.36) можно прочитать следующим образом:

Секундная убыль или прирост массы в объеме V определяется расходом вещества через поверхность, ограничивающую данный объем.

2. Закон количества движения

Из физики известна формулировка этого закона:

Скорость изменения количества движения некоторой материальной системы равна главному вектору всех высших сил, действующих на систему.

Обозначив 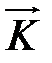суммарную величину количества движения и помня, что удельная характеристика этой величины равна произведению ρ из (4.35) находим:

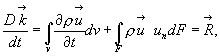(4.37)

где 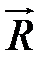- главный вектор высших сил.

Замечание:

1. Оказывается, что уравнения движения можно получить, положив в основу вместо законов Ньютона некоторые другие общие положения, в частности принцип Д’Аламбера (Даламбера), который следует из закона количества движения после введения новой величины 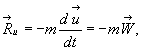, имеющая размерность силы и называемая силой инерции.

Принцип д’Аламбера для системы:

Если в любой момент времени к каждой из точек системы кроме действующих на нее высших и внутренних сил присоединить соответствующие силы инерции, то полученная система сил будет уравновешенной и к ней можно применить все уравнения статики.

Или в другой формулировке:

Равнодействующая всех сил (поверхностных и массовых), приложенных к жидкости в объеме V, должна быть равна нулю.

2. Для практического применению формулы (4.37) бывает полезно выделить из всех внешних сил отдельно силы давления, определяемые интегралом

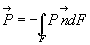(4.38)

здесь знак минус указывает ,что давление направлено (действует) не по внешней нормали 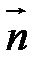, а по внутренней.

Вводя этот интеграл в формулу (4.37), получим:

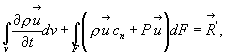(4.39)

где 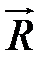^’ – обозначен главный момент всех прочих сил, исключая силы давления.

3. Закон моментов количества движения

Из физики известна формулировка этого закона:

Скорость изменения суммарного момента количества движения системы материальных тел относительно произвольно выбранной точки равна главному моменту относительно той же точки внешних, приложенных к этой системе сил.

Если через 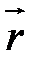обозначим координату любой частички жидкости по отношению к выбранной точке отсчета момента, то произведение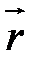 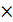ρ в общем виде представляет удельный момент количества.

Обозначив 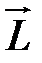суммарный момент количества движения и используя формулы (4.35) и (4.38), получим искомую интегральную запись закона моментов количества движения

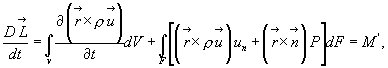(4.40)

где М^’ – обозначает момент прочих сил (сил трения, упругости, тяжести и т.д.) без сил давления, т.к. главный момент сил давления включен в формулу (4.40) в виде второго слагаемого под знаком интеграла по контрольной поверхности F.

Замечания к разделу:

Интегральные уравнения позволяют решать многие технические задачи балансового характера, когда по известным потокам одних величин вычисляются другие.

Однако основной задачей гидродинамики являются описание процесса течения жидкости, т.е. выражения связи между различными параметрами потока в различных точках пространства и во времени. Эти знания добываются путем решения дифференциальных уравнений фундаментальных законов физики, описывающих сложный процесс жидкости.