Дифференциальное уравнение закона сохранения материи (Уравнение сплошности или неразрывности)

Возьмем интегральную форму записи этого закона (формула 4.36) и преобразуем поверхностный интеграл в объемный с помощью формулы Остроградского (3.40)

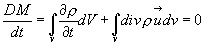
Объединяя оба объемных интеграла в один, получаем:

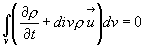
Поскольку dV 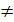и область V произвольна, то нулем оказывается подынтегральная функция. Следовательно, имеем точное дифференцированное уравнение:

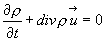(4.41)

Замечание:

1. Физический смысл закона сохранения материи вытекает (следует) из физического смысла div ρ и заключается в том, что в любой точке пространства, занятого текущей жидкостью, изменения ее плотности во времени обусловлено накоплением или стоком жидкости в смежные области.

2. Формуле (4.41) можно придать другой вид после следующих преобразований:

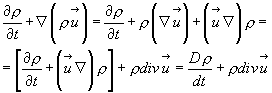(4.41а)

т.е. 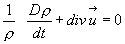(4.41б)

Поскольку div можно трактовать как скорость относительного изменения объема малой частицы жидкости неизменной массы, то уравнение неразрывности в записи (4.41б) можно прочитать так:

Скорость относительного изменения плотности частицы неизменной массы равна с обратным знаком скорости относительного изменения ее объема.

3. Если течение установившееся, то зависимости (4.41а) и (4.41б) приводятся к виду

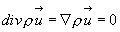(4.42)

4. Для несжимаемой жидкости (при ρ=const) закон сохранения материи записывается:

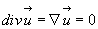(4.43)

Причем эта формула справедлива как для установившегося движения, так и для неустановившегося.

5. Несмотря на то, что уравнения (4.41) … (4.43) даны в векторной символике, тем не менее они являются соотношениями скалярными и никаких проекций на оси координат из них составить нельзя.

Обычную форму записи этих уравнений легко получить, если обратиться к координатному представлению оператора Гамильтона на основе формулы (3.32). В этом случае уравнение (4.41) имеет вид

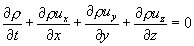(4.44)