Субстанциональное изменение количественного параметра конечной массы вещества

При отыскании математической записи основных законов физики части проводится одинаковая серия рассуждений. Чтобы не повторять их каждый раз отдельно, целесообразно сделать эти рассуждения в обобщенном виде, чтобы в дальнейшем просто пользоваться готовыми результатами.

Для этого необходимо еще раз расширить понятие субстанциональной производной.

Предварительные замечания:

В физике (термодинамике) все параметры системы разделяются на две категории:

1. интенсивные или качественные,

2. экстенсивные или количественные.

К первой группе относятся температура, давление, напряжение различных сил, скорость.

Ко второй группе относятся масса, объем, внутренняя энергия, энтропия, количество движения и т.д.

Различие между этими группами заключается в том, что количественный параметр, характеризующий всю систему (конечную массу вещества), может быть представлен, как сумма таких же величин отдельных ее частей.

Например:

Внутренняя энергия некоторой массы жидкости равна сумме внутренних энергий составляющих эту массу частиц.

Но температуру или скорость той же массы жидкости нельзя представлять как сумму температур или скоростей ее отдельных элементов. Здесь можно говорить лишь о средней температуре или скорости.

Однако среднее значение интенсивных параметров понятие несколько неопределенное (обоюдоострое). Иногда оно дает удовлетворительное представление о состоянии системы, а в ряде случаев может ввести в заблуждение. Поэтому в гидродинамике избегают пользоваться средними величинами для больших количеств жидкости (конечной массы вещества).

Замечание:

1. Для бесконечно малых объемов, где средние значения качественного параметра незначительно отличаются от его истинного значения в любой точке объема его применение вполне допустимо. Поэтому переход к рассмотрению бесконечно малых (элементарных) объемов жидкости и вызван стремлением использовать все макроскопические параметры, как количественные, так и качественные.

2. Если же ориентироваться лишь на количественные величины, то их вполне можно применять к конечным размерам или массам системы и, следовательно, можно говорить об их субстанциональном изменении для всей рассматриваемой части движущейся среды.

Рассмотрим непосредственное вычисление субстанциональное изменение некоторого количественного параметра П конечной массы жидкости М.

Будем использовать тензорное обозначение для этого параметра, так как количественная характеристика, вообще говоря, может быть тензором любого ранга.

Для выражения удельного значения того же параметра, т.е. отнесенного к единице объема, применим символ π, помня, что удельная величина может изменяться внутри данного объема от одной точки к другой.

В соответствии с самим смыслом количественного параметра можем записать очевидное соотношение

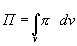(4.31)

Замечание:

Если даже выделенный в жидкости объем V, ограничивающий массу М, неподвижен, то в нем с течением времени может происходить изменение параметра П под действием внешних причин или вследствие процессов, которые развиваются внутри самого объема. Такое изменение параметра П за малое время dt, вызванное нестационарностью процесса, определяют равенством

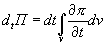(4.32)

Здесь интервал времени dt вынесен за знак интеграла потому, что он взят одинаковым для всех элементарных объемов dV, составляющих V.

Рассмотрим движение объема V в пространстве.

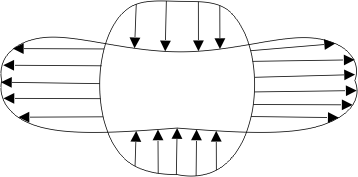
За время dt он как-то переместился относительно своего старого положения и несколько деформируется, как это показано на рис. 1

II

I

II

I

F1

F2

F2

Vоб

Условно контур I, представляющий объем V, преобразуется в контур II.

Если в начальный момент времени значение параметра П определялось выражением (4.31), то в последующий момент этот параметр примет значение П^’, которое, по аналогии с (4.31), находится тем же способом. При этом значение π заменяется на π^’, являющегося измененной величиной удельного параметра в момент времени t+dt.

Т.о. вследствие всех превращений, которые произошли с рассматриваемой массой жидкости при ее движении в пространстве, суммарная количественная характеристика претерпит такое изменение:

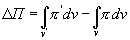(4.33)

Ввиду малости промежутка времени Vt положение и конфигурация объема V^’ будет мало отличаться от положения и объема V.

Очевидно, что состояния I и II будут иметь общую часть объема V_об (см. рис. 1).

Часть объема V уже не будет принадлежать V. Эту область пространства обозначим ΔV₁ (см. рис. 1 – часть заштрихованная стрелками внутрь в направлении перемещения поверхности, ограничивающей выделенную массу жидкости М).

Жидкость в состоянии II занимает новые области пространства ΔV_II (см. рис. 1 – часть заштрихованная стрелками наружу), ранее не принадлежавшего массе М.

Очевидно, что в соответствии со сделанными обозначениями, приращение ΔП можно записать иначе чем (4.33):

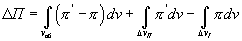(3.34)

т.о. равенство (4.34) показывает, что разность ΔП представляется суммой трех членов:

1. изменения, связанного с превращением параметра П во времени внутри неподвижной общей части объема V_об;

2. увеличение П из-за интегрального приращения объема в состоянии II;

3. уменьшение П вследствие интегральной потери в состоянии II/

Первое слагаемое на основании равенства (4.32) можно представить с точностью до бесконечно малых высших порядков с помощью зависимости

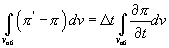
элемент второго слагаемого при достаточно малом Δt определяется выражением

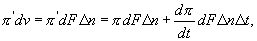
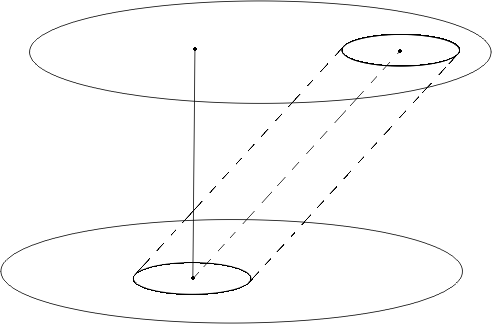
которое следует из рассмотрения рис. 2.

∆n

F'

F

M

M’

dF

рис. 2.

Действительно точка М, лежащая в момент времени t на элементе dF пограничной поверхности F в состоянии I, за время Δt переместится на пограничную поверхность F^’ в точку M^’, отвечающую состоянию II. Поэтому все соседние точки среды будут лежать на поверхности F^’ в окрестности точки M^’, а все точки, которые за время Δt пройдут через dF из объема V в объем V^’, заполняет (элемент объема dV) косой цилиндр с основанием dF и высотой .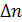

Очевидно, что новая область ΔV_II может быть составлена из таких элементов:

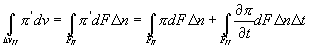
Аналогичным образом подсчитывается и последний интеграл в равенстве (4.34) т.е.

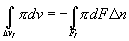
Здесь знак минус указывает, что в данном случае нормаль направлена внутрь объема V.

Т.к. части F_I и F_II составляют всю поверхность F, ограничивающую массу М в состоянии I, то поэтому разность двух последних челнов в правой части уравнения (4.31) можно записать следующим образом:

(*)

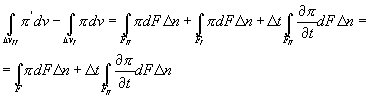Пользуясь выражением (*) и перейдя к пределу в отношении 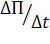при Δt → 0, получим субстанциональную производную 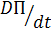, выражающую скорость изменения параметра П рассматриваемой массы жидкости, т.е.

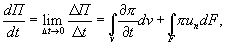(4.35)

где 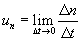- есть скорость по нормали к поверхности F.

При этом все остальные слагаемые при переходе к пределу при Δt → 0 пропадают, являясь бесконечно малыми высших порядков по сравнению с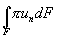

Замечание:

1. Соотношение (4.35) показывает, что полное изменение интегральной величины П по времени состоит из ее местного изменения в фиксированном объеме V и потока этой величины через поверхность, ограничивающую указанный объем в данный момент времени.

Здесь под потоком любой величины через поверхность F понимаем интеграл вида

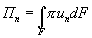
2. Субстанциональная производная складывается из локальной и конвективной составляющих.