Обобщение понятия субстанциональной производной бесконечно малой частицы жидкости

Проведем формальные рассуждения.

В общем случае движения жидкости имеются переменные во времени, которые рассматриваются как параметры жидкости.

Изменение какого-либо параметра можно представить как следствие, вытекающее из рассмотрения его в смежной точке пространства и в смежный момент времени.

Поэтому полное приращение d… определяется суммой двух приращений: временного d_t … и пространственного d_r…

Приращение во времени при фиксированных координатах определяется символическим равенством:

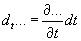
Пространственное изменение скалярного или векторного параметров на основании формул (3.37) и (3.44) в данный момент времени находится с помощью зависимости

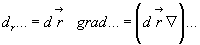
суммируя оба приращения и деля на элемент времени d_t, приходим к соотношению

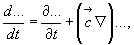
в котором 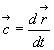есть скорость перехода от одной точки пространства к другой, т.е. скорость слежения за различными точками пространства.

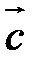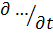Если объектом слежения выбрать какую-то частицу жидкости, тогда скорость слежения совпадает со скоростью движения этой частицы , поскольку перенос взгляда из одной точки пространства в другую будет следовать за перемещением этой массы (частички) жидкости. В этом случае производная обращается в субстанционарную производную

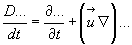(4.17)

Замечание:

Т.о. субстанционарная производная есть понятие не только математическое, но и физическое. Оно связано с изучением изменения некоторого параметра во времени при движении одной и той же массы жидкости.