Субстанциональная производная бесконечно малой частицы жидкости
Рассмотрим математические аспекты изучения установившихся и неустановившихся движений.
Пусть нас интересует некоторый параметр φ, характеризующий элементарный объем жидкости ΔV (это может быть давление, температура, скорость и т.д.).
Подсчитаем изменение этого параметра за малый промежуток времени Δt.
В соответствии с общими правилами дифференциального исчисления можем записать равенство
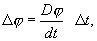 (4.11)
(4.11)
в котором символ D употреблен вместо обычно применяемого знака дифференциала d, для того, чтобы подчеркнуть то обстоятельство, что производная относится к одной и той же массе жидкости, заключенной внутри объема ΔV.
Такая производная называется субстанциональной производной (от слова субстанция – вещество). Ее еще называют либо полной производной, либо вещественной, либо эйлеровой.
Для установившегося и неустановившегося движения эта производная вычисляется различным образом.
1. Случай установившегося движения.
Пусть за время Δt частица жидкости переместится вдоль своей траектории на элемент длины Δ 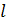 и попадет в другую точку пространства, где параметр φ отличается от исходного значения на величину Δφ.
и попадет в другую точку пространства, где параметр φ отличается от исходного значения на величину Δφ.
Замечание:
По определению при установившемся течении в каждой отдельно взятой точке ни один параметр не меняет своего значения с течением времени. Поэтому приращение Δφ будем рассматривать просто как следствие различных положений объема ΔV в пространстве вне зависимости от времени его движения.
Т.к. одна точка от другой в рассматриваемом случае отстоит на расстоянии Δ 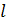 , то справедливо очевидное равенство
, то справедливо очевидное равенство
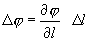 (4.12)
(4.12)
Приравняв формулы (4.11) и (4.12), поделив на время Δt и перейдя к пределу при Δt → 0, получим искомую формулу для субстанционарной производной для установившегося движения: 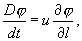 (4.13)
(4.13)
где 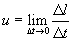 - скорость движения частицы.
- скорость движения частицы.
2. Случай неустановившегося движения
Рассмотрим формулу (4.12). Это равенство учитывает различие параметров потока в двух соседних точках пространства в один и тот же момент времени.
При неустановившемся движении за время Δt, пока объем ΔV перемещается из одной точки в другую, параметр φ изменится в сравнении с тем его значением, которое он имел бы при установившемся движении.
Это дополнительное приращение может быть подсчитано по формуле
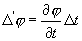 (4.14)
(4.14)
Т.о. полное изменение параметра φ составит
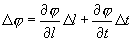 (4.15)
(4.15)
Приравняв формулы (4.15) и (4.11), поделив на время Δt и перейдя к пределу при Δt → 0, получим искомую формулу для субстанционарной производной при неустановившемся режиме течения жидкости
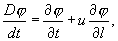 (4.16)
(4.16)
где 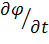 - называется локальной (местной) производной,
- называется локальной (местной) производной,
и 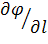 – называется конвективной производной,
– называется конвективной производной,
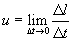 - скорость движения частицы.
- скорость движения частицы.
Замечание:
Символически равенство (4.16) можно записать
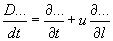
здесь точки, стоящие за знаком приращения, заменяют написание рассматриваемого параметра и служат для общности рассуждений.
Символ 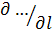 представляет собой производную по направлению скорости движения частицы. Это направление, при одномерной постановке задачи, всегда считается известным, поэтому и скорость движения частицы и рассматривается как скалярная величина.
представляет собой производную по направлению скорости движения частицы. Это направление, при одномерной постановке задачи, всегда считается известным, поэтому и скорость движения частицы и рассматривается как скалярная величина.
В условиях сложного пространственного движения (сплошной среды) жидкости данное представление о субстанциональной производной необходимо расширить и обобщить.
Дата добавления: 2019-12-09; просмотров: 1008;











