АВС – метод анализа запасов
| Наименование вида сырья | Стоимость сырья, тыс. руб. | Удельный вес, % | Совокупный процент | Категория |
| Всего | ||||
| Сырье1 | 29,9 | 29,9 | А | |
| Сырье2 | 16,4 | 46,3 | А | |
| Сырье3 | 13,1 | 59,4 | А | |
| Сырье4 | 9,8 | 69,2 | В | |
| Сырье5 | 6,3 | 75,5 | В | |
| Сырье6 | 5,2 | 80,7 | В | |
| Сырье7 | 3,8 | 84,5 | В | |
| Сырье8 | 3,6 | 88,1 | В | |
| Сырье9 | 2,3 | 90,4 | В | |
| Сырье10 | 1,9 | 92,2 | С | |
| Сырье11 | 1,2 | 93,5 | С | |
| И другие 142 вида сырья | 6,5 | С |
В полученном списке выделим 3 группы сырья по категориям:
- категория А – 3 вида сырья, стоимость которого составляет почти 60 % от общей суммы материальных ресурсов;
- категория В – 6 наименований сырья, стоимость которых составляет около 30 %;
- категория С – все остальные 144 вида сырья, удельный вес которых составляет менее 10 %.
В зависимости от специфики предприятия в аналитических целях деление на категории может быть осуществлено в других пропорциях.
Использование АВС-метода позволяет сосредоточиться на контроле только за наиболее важными видами запасов (категории А и В) и тем самым сэкономить время и ресурсы и повысить эффективность управления запасами.
Основное внимание при управлении запасами должно быть уделено 3 наиважнейшим видам сырья (категория А). Для них необходимо применять модель определения наиболее экономичного (оптимального) размера заказа.
Планирование запасов связано с определением потребности предприятия в материальных ресурсах. Для этого используется нормирование оборотных средств. В процессе нормирования устанавливают норму и норматив запасов. Норма – это относительная величина, определяемая, как правило, в днях. Норматив исчисляется на основании среднедневного расхода материальных ресурсов (Р) и средней нормы запаса в днях.
В норме запаса по каждому виду материальных ресурсов учитывается время пребывания в текущем (Т), страховом (С), транспортном (М), технологическом (А), подготовительном (Д) запасах.
Таким образом, норматив оборотных средств в запасах материальных ресурсов (Н) определяется по формуле
Н = Р(Т + С + М + А + Д). (6.12)
При управлении запасами у предприятия возникает проблема их оптимизации. Суть ее вербально может быть описана следующим образом. Известно, что на предприятиях существует производственный запас сырья и материалов. В то же время можно условно договориться, что запас не создается, а предприятие будет покупать соответствующие материалы изо дня в день по мере необходимости. В этом случае возникают следующие проблемы: во-первых, предприятию придется платить более высокие цены за маленькие партии товаров; во-вторых, существует риск кратковременной остановки производства в случае непоставки сырья и материалов вовремя. Поэтому предприятия формируют запасы материальных ресурсов, несмотря на издержки по их хранению, связанные со складскими расходами, с порчей, а также омертвлением денежных средств, вложенных в запасы. В этой связи возникает потребность поиска оптимальной величины запасов, которая обеспечила бы эффективность их использования и бесперебойность производственного процесса.
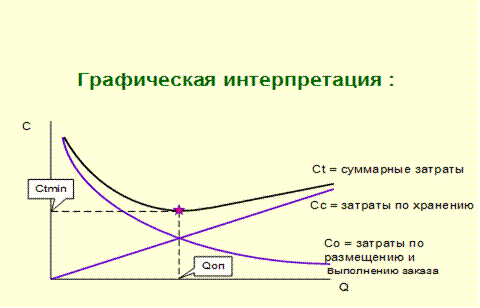
Решение любой оптимизационной задачи связано с определением целевого критерия. Этим критерием могут выступать затраты, связанные с поддержанием запасов, состоящие из двух компонентов: затраты по хранению материальных ресурсов и затраты по размещению и выполнению заказов. Оба компонента общих затрат, связанных с поддержанием запасов, изменяются обратно пропорционально друг другу. С ростом размера запасов увеличиваются затраты по хранению. Чем больше завезенная партия сырья и материалов, тем в большем объеме требуются складские помещения для хранения, возрастают затраты электроэнергии, увеличивается естественная убыль и т. п. Кроме того рост запасов сопровождается и ростом затрат на поддержание соответствующих источников финансирования. В то же время затраты по размещению и выполнению заказов ведут себя иначе. При увеличении партии заказа снижаются транспортные расходы, расходы на размещение заказа и т. п., приходящиеся на единицу запасов. На рис. 6.11 представлены линии затрат, связанных с хранением и выполнением заказов, а также суммарные затраты, связанные с поддержанием запасов. Кривая суммарных затрат имеет точку минимума, в которой и может быть определен оптимальный (экономичный) размер заказа. Эта точка может быть найдена путем дифференцирования функции суммарных затрат (нахождение точки экстремума).
Для решения данной задачи введем обозначения:
Q – размер заказываемой партии запасов, ед.;
D – годовая потребность в материальных ресурсах, ед.;
F – затраты по размещению и выполнению одного заказа (предполагаются постоянными), руб.;
H – затраты по хранению единицы производственных запасов, руб.;
Cc – затраты по хранению, руб.;
Co – затраты по размещению и выполнению заказа, руб.;
Ct – общие (суммарные) затраты, руб.
 .
.
Рис.6.11. Модель оптимального размера заказа
Допустим, предприятие придерживается следующей политики: по мере исчерпания запасов поступает очередная партия сырья и материалов размером в Q единиц.
В этих условиях средний размер запасов будет равен Q/2 (рис.6.12), количество заказанных и полученных партий сырья и материалов за год составит D/Q, а суммарные затраты по поддержанию запасов могут быть найдены по формуле
Сt = Cc + Co = H×Q/2 + F×D/Q. (6.13)

Рис.6.12. Определение среднего объема запасов
Как видно из графика, функция y = f(Q) имеет вид параболы, поэтому, дифференцируя по Q, можно найти такое его значение, при котором функция достигает своего минимума. Таким образом, формула расчета размера оптимальной партии заказа (Qоп) примет вид
Qоп = 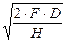 . (6.14)
. (6.14)
Используя эту формулу предприятие может планировать оптимальный (экономичный) размер заказа, точку его возобновления, а также время выполнения, что будет способствовать решению проблемы оптимизации запасов (рис.6.13).
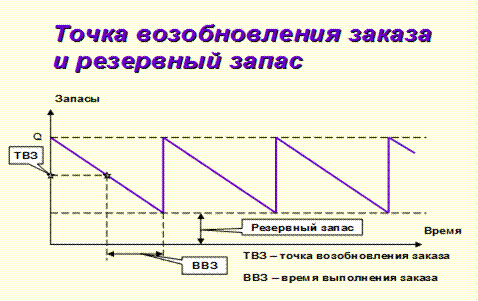
Рис. 6.13. Определение точки возобновления заказа
Дата добавления: 2020-11-18; просмотров: 800;











