Grad Р (градиент давления)

Пусть под скаляром мы будем понимать давление P.

Рассмотрим подынтегральное выражение входящее в формулу (3.18)

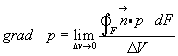
Под знаком интеграла содержится произведение p∙dF, которое дает величину силы давления, приложенного к площадке dF.

После умножения не единичный нормальный вектор 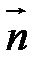получаем направление действия этой силы, поскольку давление всегда действует по нормали к рассматриваемой площадке.

Выделим в пространстве некоторый объем ΔV или будем рассматривать одну и ту же массу жидкости, занимающую объем ΔV, (в данном случае различие точек зрения не меняет смысла понятия градиента давления), тогда величина - 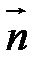pdF дает величину и направление силы давления на этот объем по площадке dF.

Знак минус поставлен на том основании, что давление действует всегда по внутренней нормали, а в формуле рассматривается внешняя нормаль 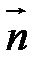к поверхности, охватывающей объем ΔV.

Проинтегрируем теперь по замкнутой поверхности F и получим суммарную силу давления на объем ΔV:

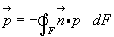(3.21)

Разделив равенство (3.21) на величину объема ΔV, получим среднее значение силы давления, действующей на единичный объем, заключенный внутри поверхности F.

При ΔV → 0 предел этого отношения дает точное значение величины и направления суммарной силы давления, которой подвергается единичный объем, охватывающий интересующую нас точку пространства или центр инерции движущейся бесконечно малой частички жидкости.

3.2.3 rot 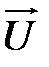(ротор скорости)

Анализируя выражение (3.19), т.е.

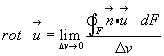
и рассматривая частицу жидкости произвольной формы, как это делали при обсуждении div 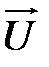и grad P, невозможно дать физическое трактование rot .

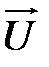Замечание: rot 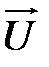представляет собой удвоенную угловую скорость вращения частицы жидкости в рассматриваемой точке пространства, т.е.

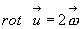(3.22)