Идеальный газ в недеформируемом пласте

Выразим скорость через приведённый объёмный расход:

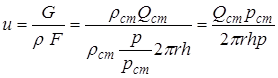. (8.4)

Подставив выражение (8.4) в (8.1), находим:

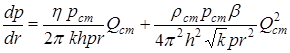. (8.5)

Разделив переменные, и, проинтегрировав в пределах от рдор_с и от rдоr_c , имеем:

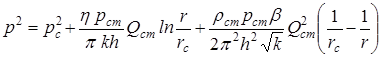. (8.6)

Распределение давления по (8.6) отличается от распределения давления по закону Дарси наличием последнего члена, что ведет к более резкому изменению давления в призабойной зоне.

Интегрируя уравнение(8.5) в пределах от р_кдор_с и от R_кдоr_c ,получим выражение (при пренебрежении 1/R_к по сравнению с 1/r_c) :

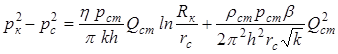, (8.7)

или в общепринятом виде:

. (8.8)

Коэффициенты Аи Вопределяют по данным исследования скважин при установившихся режимах.

Однородная несжимаемая жидкость в деформируемом (трещиноватом) пласте

Для трещиноватой среды двухчленный закон записывается в виде:

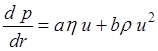, (8.9)

где 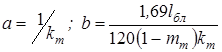; l_бл - средний линейный размер блока.

Умножив слагаемые (8.9) на плотность rи вынеся за скобки вязкость h, применительно к плоскорадиальному потоку, получим:

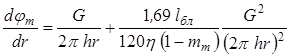, (8.10)

где .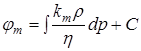

После разделения переменных и интегрирования (8.10) в пределах от r_cдоr_к иот j_сдоj_к , получим:

(8.11)

Если в (8.11) подставим выражение для трещинной проницаемости, то будем иметь выражение:

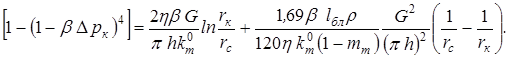(8.12)