ЛЕКЦИЯ 7 ОСНОВНЫЕ ЗАВИСИМОСТИ ОДНОМЕРНОЙ ФИЛЬТРАЦИИ

Для практического исследования фильтрационных потоков, следующих линейному закону Дарси, необходимо знать конкретные физические параметры – давления, скорости и т. д.

Для разработки месторождений наибольшее значение имеет плоско-радиальный тип течения (приток к скважине). Поэтому получим указанные зависимости для плоскорадиального потока.

Исходные уравнения:

притока: 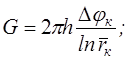(7.1)

изменения потенциальной функции:

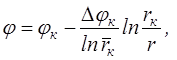(7.2)

где ;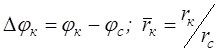

изменения градиента потенциала:

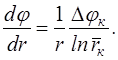(7.3)

7.1 Течение несжимаемой жидкости через недеформируемый пласт

В данном случае k = const, r = const , h = const:

.

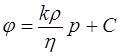Подставляя последнее уравнение в (7.1), получим формулу Дюпюи объемного дебита скважины:

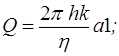
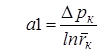
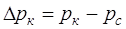(7.4)

Из (7.4) следует, что дебит пропорционален депрессии 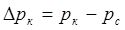. График зависимости Q от 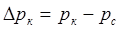(рисунок 7.1) называется индикаторной диаграммой. Отношение дебита к депрессии называется коэффициентом продуктивности скважины:

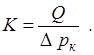(7.5)

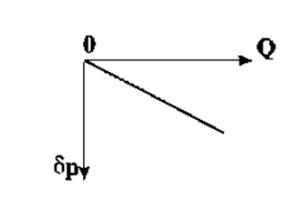
Рисунок 7.1 – Индикаторная диаграмма плоскорадиального потока несжимаемой жидкости по закону Дарси

Дебит слабо зависит от величин радиусов контура питания и скважины, так как их отношение входит в формулу под знаком логарифма.

Подставляя параметры пласта и жидкости в (7.2), получаем выражение распределения давления в пласте:

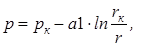
где 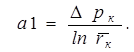(7.6)

Графиком зависимости р=р(r) является логарифмическая кривая (рисунок 7.2), вращением которой вокруг оси скважины образуется поверхность, называемая воронкой депрессии. Отсюда видно, что основное влияние на дебит оказывает состояние призабойной зоны. Поэтому улучшение ее состояния обеспечивает эффективность методов интенсификации притока.

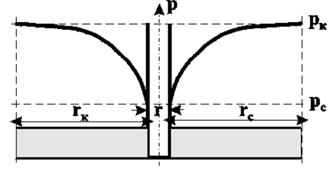
Рисунок 7.2– График распределения давления в плоскорадиальном фильтрационном потоке

Изобары – концентрические, цилиндрические поверхности, ортогональные траекториям.

Аналогично находим выражения для градиента давления в пласте:

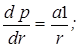(7.7)

и скорости фильтрации:

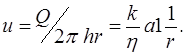(7.8)

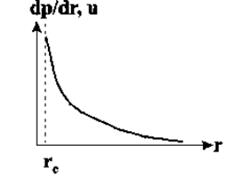
Рисунок 7.3– График зависимости градиента давления и скорости фильтрации от расстояния до центра скважины

Градиент давления и скорость фильтрации обратно пропорциональны расстоянию (рисунок 7.3) и образуют гиперболу с резким возрастанием их значений при приближении к забою.

Движение частицы описывается уравнением:

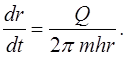
Интегрируем данное соотношение по времени от 0 до tи по расстоянию от R₀до r, где R₀– начальное положение частицы флюида. Получим:

.

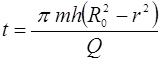Время отбора всей жидкости из кругового пласта:

.

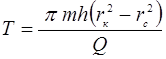Средневзвешенное давление в пласте определится:

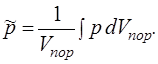(7.9)

С целью получения выражения для него определим объем пор пласта и запишем его дифференциал:

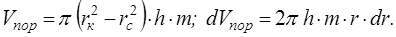
Подставим их в (7.9), проинтегрируем от r_cдо r_к. Пренебрегая r_с по сравнению с r_к ,получим:

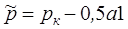. (7.10)