ОПРЕДЕЛЕНИЕ НЕИЗВЕСТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

В процессе эксплуатации продукции или специальных испытаний на надежность возникает необходимость экспериментально оценить неизвестные параметры, как например, среднее время безотказной работы Т_о; среднее время восстановления Т_в; интенсивность отказов 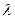и т. п.

Методика и последовательность решения задачи статистической оценки различных неизвестных параметров имеет определенную общность. Рассмотрим решение задачи экспериментальной оценки неизвестного параметра безотказности Т_о некоторой радиолокационной системы, испытываемой в процессе эксплуатации.

Так как величина Т_о является математическим ожиданием случайной величины Т — времени безотказной работы между отказами, т. е.

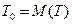
то, естественно, для оценки параметра Т_о необходимо в качестве исходных статистических данных располагать фактическими частными реализациями случайной величины Т, т. е. иметь набор опытных данных: ^.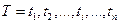

В каждой из случайных величин 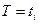содержится определенная информация о законе распределения случайной величины Т и о ее математическом ожидании Т_о. В отличие от оценки неизвестного закона F(t), когда требовался большой объем статистических данных (n >100), число п реализаций T =t_i при оценке Т_о может быть любым, в том числе и малым. Однако при малой статистике точность и достоверность оценки могут оказаться недостаточными, поэтому обычно требуют, чтобы число реализаций п при оценке параметра Т_о было бы больше десяти, хотя и при меньших п можно указать соответствующие точность и достоверность оценки.

В процессе статистической оценки определяется не сама неизвестная величина Т_о, а ее опытное значение или точечная оценка 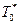, причем .

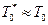Это приближенное вероятностное равенство тем точнее и достовернее, чем больший объем исходной статистики используется для расчета экспериментальной величины 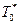. Так как для расчета опытной величины 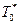используются частные реализации случайной величины 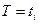, то и сама 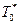является случайной величиной. Этим объясняется характер приближенного равенства .

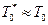Задачу оценки неизвестного параметра Т_о сформулируем следующим образом.

Дан некоторый набор п исходных статистических данных 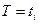, при i=l, 2, 3,..., п.

Требуется оценить неизвестный параметр безотказности T₀

Решение. Для правильной и полной статистической оценки неизвестного параметра Т_о по результатам эксперимента необходимо:

А. определить, по какой формуле рассчитывать наилучшую статистическую оценку для неизвестного параметра T₀ , используя исходную статистику;

Б. определить какова достоверность и точность получаемой оценки.