ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Одной из главных задач обеспечения и постоянного повышения характеристик качества продукции и процессов является использование методов и средств теории вероятностей и математической статистики. Мощным инструментом регулирования и управления качеством служит набор методов, входящих в понятие FMEA ( Failure Mode and Effects Analysis) – анализ видов отказов и их воздействий. Все эти методы невозможно применять без начальных знаний основ математической статистики. Поэтому в данном разделе приводятся необходимые начальные сведения по математической статистике (Л.2,4).
Теория вероятности выводит свойства реального физического процесса из математической модели, т.е., определяет какой процент интересующих наблюдений, находится в выборке.
Теория математической статистики устанавливает свойства математической модели на основании данных наблюдения, т.е. распространяет данные выборки на всю генеральную совокупность.
Статистика позволяет оценить случайность или закономерность проведенных измерений за счет описания массива экспериментальных данных, оценивания характеристик (моментов или статистик) массива данных и принятия решений на основе определенных статистик.
В теории математической статистики одним из основополагающих понятий является выборка, характеризующаяся объемом, функцией распределения членов выборки и правилами создания. Обычно стараются создавать репрезентативную (представительную) выборку, т.е. такую, когда любая комбинация из равного числа элементов генеральной совокупности имеет равную вероятность образовать выборку. Обычно, отдельное значение случайной переменной обозначается через x, а ее реализацию через X. С этих позиций, генеральная совокупность представляет собой множество всех возможных реализаций случайной переменной, а выборка представляет n- мерную реализацию, состоящую из n- исходов.
Каждая переменная x с определенной вероятностью может принять какое либо значение, тогда накопленное распределение вероятностей F(x), чаще всего называемое функцией распределения может быть записано в виде:
F(x) = P(X 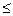 x). 4
x). 4
В случае дискретной случайной переменной ( количество дефектных деталей, количество обслуженных посетителей и т.п.) соответствие между xi и вероятностью (относительной частотой ) f(xi) представляется в виде полигона частот или гистограммы. Ломаная линия, соединяющая середины верхней части прямоугольников гистограммы, площадь под которой примерно равна единице,называется функцией вероятности или частотной функцией. Выражение для функции распределения может быть записано в виде:
. 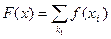 5
5
На рисунке 14 дана иллюстрация гистограммы и полигона частот

Рис.14. Иллюстрация гистограммы и полигона частот
Для непрерывной случайной переменной функция распределения запишется в виде:
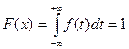 6
6
где f(t) плотность вероятности.
В том случае, когда необходимо рассмотреть изменение случайной переменной в интервале от а до b выражение (6) примет вид:
P(a≤X≤b) = F(b) – F (a) = 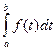 7
7
т.е. вероятность события на этом интервале равна площади под кривой функции распределения в заданных пределах. Чаще всего, функция распределения, определяемая в пределах, носит название закона распределения. Подробнее о законах распределения следует читать в специальной литературепо математической статистике или в ППП «Статистика» или в главе МАТЛАБ по статистике.
Подводя итог сказанному, следует запомнить, что любая случайная переменная полностью определяется функцией или законом распределения!
Однако при проведении эксперимента или оценке характеристик качества, когда получена начальная выборка, состоящая из какого-то числа данных, нельзя судить о возможном распределении. Поэтому, на основе полученной выборки следует оценить числовые характеристики (статистики) распределения вероятностей, называемые моментами E порядка k, которые представляют собой математическое ожидание М вида:
E =M(X -x)k, k= 1,2,3,… 8
Следует иметь в виду, что для обозначения характеристик - генеральной - ГС и выборочной совокупностей - ВС, применяются различные символы, которые представлены в таблице 5.
В соответствии с этими символами будут приводиться все дальнейшие обозначения.
Таблица 5. Обозначения, применяемые для статистик ГС и ВС
| Совокупность | Среднее | Дисперсия | Стандартное | Корреляция | Объем | Размах |
| Генеральная | 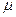
| D, V | 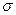
| 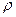
| N | --- |
| Выборочная | 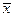
| S, s2 | s | r | n | R |
В таблице 6 приведены основные статистики (моменты), для начальной оценки экспериментальных данных.
Таблица 6. Определение четырех моментов распределения
| Моменты | Применимость | Статистика | Значение |
| Е1 | Меры положения | Среднее: -арифметическое, -геометрическое, - гармоническое. Медиана. Мода. | Математическое ожидание среднего значения-М Срединное значение,квантиль1/2 Максимум распределения |
| Е2 | Меры рассеяния | Дисперсия. Стандартное отклонение. Размах. | Отклонение от М, D=M(x- 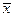 )2
Корень квадратный из дисперсии
R= x max - xmin )2
Корень квадратный из дисперсии
R= x max - xmin
|
| Е3 | Меры формы | Асимметрия | Отсутствие симметрии относительно нормального распределения- N |
| Е4 | Эксцесс | Различие между N и распределением x, плоско или островершинность |
В задачах оценки качества чаще всего применяются четыре непрерывных законов распределения: Муавра - Лапласа - Гаусса (нормальное или N -распределение, Стьюдента (Госсета)(t- распределение), Пирсона - Хельмерта ( 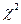 - распределение), Фишера (F- распределение). Применимость этих распределений представлена в таблице 7.
- распределение), Фишера (F- распределение). Применимость этих распределений представлена в таблице 7.
Нормальное распределение зависит от математического ожидания и стандартного отклонения, остальные три от числа степеней свободы - ЧСС, обозначаемой 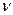 или r. ЧСС статистически определяется числом независимых (свободных) наблюдений и равно объему выборки минус число статистик, оцениваемых по данной выборке, тогда
или r. ЧСС статистически определяется числом независимых (свободных) наблюдений и равно объему выборки минус число статистик, оцениваемых по данной выборке, тогда
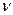 = n - m, 9
= n - m, 9
где m- число определяемых статистик. Чем меньше 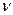 , тем сильнее отклонение от нормального распределения и хвосты распределений больше.
, тем сильнее отклонение от нормального распределения и хвосты распределений больше.
Таблица 7. Применимость различных распределений
| F | Назначение | Сходимость к N | Статистика f(x) |
| N | Описание членов ГС или ВС | --- | 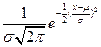
|
| t | Сравнение средних значений ГС и ВС | Симметрично, похоже
на N,зависит от 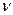 ,
сходится к N при ,
сходится к N при 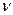 =10 =10
| 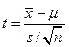
|
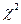
| Сравнение дисперсий ГС и ВС | Зависит от 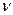 ,сходится
к N при ,сходится
к N при 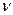 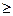 50 50
| 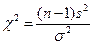
|
| F | Определение принадлежности разных выборок к ГС | Асимметрично, зависит
от 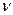 , сходится к N при
специальных условиях , сходится к N при
специальных условиях
| 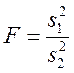
|
При увеличении номера момента, число статистик возрастает, так при определении дисперсии таких статистик одна - среднее значение, и 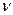 =n-1 , при рассмотрение принадлежности двух выборок одной ГС,
=n-1 , при рассмотрение принадлежности двух выборок одной ГС, 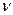 =n - 2 и т.д.
=n - 2 и т.д.
В последней графе таблицы 7 приведены аналитические выражения для статистик.
Дата добавления: 2021-07-22; просмотров: 555;











