Этапы создания математических моделей
В общем случае под математической моделью объекта (системы) понимается любое математическое описание, отражающее с требуемой точностью поведения объекта (системы) в реальных условиях. Математическая модель отражает записанную на языке математики совокупность знаний, представлений и гипотез исследователя о моделируемом объекте. Поскольку эти знания никогда не бывают абсолютными, то модель лишь приближенно учитывает поведение реального объекта.
Математическая модель системы – это совокупность соотношений (формул, неравенств, уравнений, логических соотношений), определяющих характеристики состояний системы в зависимости от ее внутренних параметров, начальных условий, входных сигналов, случайных факторов и времени.
Процесс создания математической модели можно разбить на этапы отраженные на рис. 3.2.
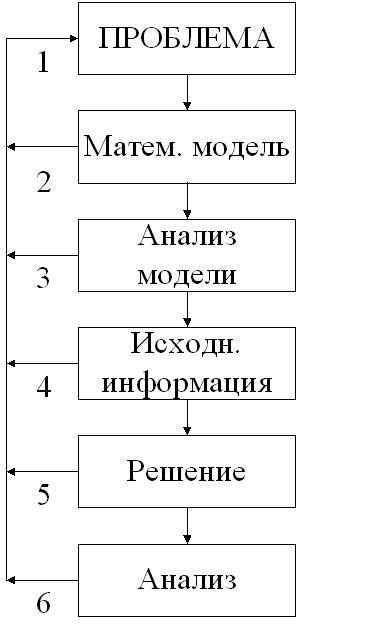
Рис. 3.2 Этапы создания математической модели
1. Постановка проблемы и ее качественный анализ. Этот этап включает:
· выделение важнейших черт и свойств моделируемого объекта и абстрагирование от второстепенных;
· изучение структуры объекта и основных зависимостей, связывающих его элементы;
· формирование гипотез (хотя бы предварительных), объясняющих поведение и развитие объекта.
2. Построение математической модели. Это – этап формализации проблемы, выражения ее в виде конкретных математических зависимостей и отношений (функций, уравнений, неравенств и т.д.). Обычно сначала определяется основная конструкция (тип) математической модели, а затем уточняются детали этой конструкции (конкретный перечень переменных и параметров, форма связей). Таким образом, построение модели подразделяется в свою очередь на несколько стадий.
Неправильно полагать, что чем больше факторов (т.е. входных и выходных переменных состояния) учитывает модель, тем она лучше «работает» и дает лучшие результаты. То же можно сказать о таких характеристиках сложности модели, как используемые формы математических зависимостей (линейные и нелинейные), учет факторов случайности и неопределенности и т.д. Излишняя сложность и громоздкость модели затрудняют процесс исследования. Нужно не только учитывать реальные возможности информационного и математического обеспечения, но и сопоставлять затраты на моделирование с получаемым эффектом (при возрастании сложности модели нередко рост затрат на моделирование может превысить рост эффекта от внедрения моделей в задачи управления).
3. Математический анализ модели. Целью этого этапа является выяснение общих свойств модели. Здесь применяются чисто математические приемы исследования. Наиболее важный момент – доказательство существования решений в сформулированной модели (теорема существования). Если удается доказать, что математическая задача не имеет решения, то необходимость в последующей работе по первоначальному варианту модели отпадает; следует скорректировать либо постановку задачи, либо способы ее математической формализации. При аналитическом исследовании модели выясняются такие вопросы, как, например, единственно ли решение, какие переменные могут входить в решение, каковы будут соотношения между ними, в каких пределах и в зависимости от каких исходных условий они изменяются, каковы тенденции их изменений и т.д.
4. Подготовка исходной информации. Моделирование предъявляет жесткие требования к системе информации. В процессе подготовки информации широко используются методы теории вероятностей, теоретической и математической статистики. При системном математическом моделировании исходная информация, используемая в одних моделях, является результатом функционирования других моделей.
5. Численное решение. Этот этап включает разработку алгоритмов для численного решения задачи, составления программ на ЭВМ и непосредственное проведение расчетов. Здесь приобретают актуальности различные методы обработки данных, решения разнообразных уравнений, вычисления интегралов и т.п. Нередко расчеты по математической модели носят многовариантный, имитационный характер. Благодаря высокому быстродействию современных ЭВМ удается проводить многочисленные «модельные» эксперименты, изучая «поведение» модели при различных изменениях некоторых условий.
6. Анализ численных результатов и их применение. На этом заключительном этапе цикла встает вопрос о правильности и полноте результатов моделирования, об адекватности модели, о степени ее практической применимости. Математические методы проверки результатов могут выявлять некорректности построения модели и тем самым сужать класс потенциально правильных моделей.
Неформальный анализ теоретических выводов и численных результатов, получаемых посредством модели, сопоставление их с имеющимися знаниями и фактами действительности также позволяют обнаруживать недостатки исходной постановки задачи, сконструированной математической модели, ее информационного и математического обеспечения.
Поскольку современные математические задачи могут быть сложны по своей структуре, иметь большую размерность, то часто случается, что известные алгоритмы и программы для ЭВМ не позволяют решить задачу в первоначальном виде. Если невозможно в короткий срок разработать новые алгоритмы и программы, исходную постановку задачи и модель упрощают:
· снимают и объединяют условия, уменьшают число учитываемых факторов.
· нелинейные соотношения заменяют линейными и т.д.
Недостатки, которые не удается исправить на промежуточных этапах моделирования, устраняются в последующих циклах. Но результаты каждого цикла имеют и вполне самостоятельное значение. Начав исследование с построения простой модели, можно быстро получить полезные результаты, а затем перейти к созданию более совершенной модели, пополняемой новыми условиями, включающей уточненные математические зависимости.
Дата добавления: 2017-05-02; просмотров: 13280;











