Глава 3. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

Для исследования характеристик процесса функционирования любой системы математическими методами, включая и машинные, должна быть проведена формализация этого процесса, т.е. построена математическая модель.

Под математическим моделированием следует понимать процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью. Исследование этой модели, позволяет получать характеристики рассматриваемого реального объекта. Вид математической модели зависит как от природы реального объекта, так и задач исследования объекта и требуемой достоверности и точности решения этой задачи.

Любая математическая модель описывает реальный объект лишь с некоторой степенью приближения к действительности, математическое моделирование можно разделить на аналитическое, имитационное и комбинированное.

Для аналитического моделирования характерно то, что процессы функционирования элементов системы записываются в виде некоторых функциональных соотношений (алгебраических, интегральных, дифференциальных, конечно-разностных и т.п.) или логических условий.

Аналитическая модель может быть исследована следующими методами:

а) аналитическим, когда стремятся получить в общем виде явные зависимости для искомых характеристик;

б) численным, когда, не умея решать уравнений в общем виде, стремятся получить числовые результаты при конкретных начальных данных;

в) качественным, когда не имея решения в явном виде, можно найти некоторые свойства решения (например, оценить устойчивость решения).

Наиболее полное исследование процесса функционирования системы можно провести, если известны явные зависимости, связывающие искомые характеристики с начальными условиями, параметрами и переменными. Однако такие зависимости удается получить только для сравнительно простых систем. При усложнении систем исследование их аналитическим методом наталкивается на значительные трудности, которые часто бывают непреодолимыми. Поэтому, желая использовать аналитический метод, в этом случае идут на существенное упрощение первоначальной модели, чтобы иметь возможность изучить хотя бы общие свойства системы. Такое исследование на упрощенной модели аналитическим методом помогает получить ориентировочные результаты для определения более точных оценок другими методами.

Численный метод позволяет исследовать по сравнению с аналитическим методом более широкий класс систем, но при этом полученные решения носят частный характер.

Численный метод особенно эффективен при использовании компьютеров.

В отдельных случаях исследования системы могут удовлетворить и те выводы, которые можно сделать при использовании качественного метода анализа математической модели. Такие качественные методы широко используются, например, в теории математического управления для оценки эффективности различных вариантов систем управления.

При имитационном моделировании реализующий модель алгоритм воспроизводит процесс функционирования системы во времени. Имитируются элементарные явления, составляющие процесс, с сохранением их логической структуры и последовательности протекания во времени. Это позволяет по исходным данным получить сведения о состояниях процесса в определенные моменты времени, дающие возможность оценить характеристики системы.

Основным преимуществом имитационного моделирования по сравнению с аналитическим является возможность решения более сложных задач.

Имитационные модели позволяют достаточно просто учитывать такие факторы, как наличие дискретных и непрерывных элементов, нелинейные характеристики элементов системы, многочисленные случайные воздействия и др., которые часто создают трудности при аналитических исследованиях. В настоящее время имитационное моделирование – наиболее эффективный метод получения информации о поведении системы, особенно на этапе ее проектирования.

Комбинированное (аналитико-имитационное) моделирование при анализе и синтезе систем позволяет объединить достоинства аналитического и имитационного моделирования. При построении комбинированных моделей проводится предварительная декомпозиция процесса функционирования объекта на составляющие подпроцессы и для тех из них, где это возможно, используются аналитические модели, а для остальных подпроцессов строятся имитационные модели.

Математическая модель системы – это совокупность соотношений (формул, неравенств, уравнений, логических соотношений), определяющих характеристики состояний в зависимости от ее внутренних параметров – начальных условий, входных сигналов, случайных факторов и времени.

Пример: Возьмем некоторую простую систему регулирования, структурная схема которой представлена на рис. 3.1.

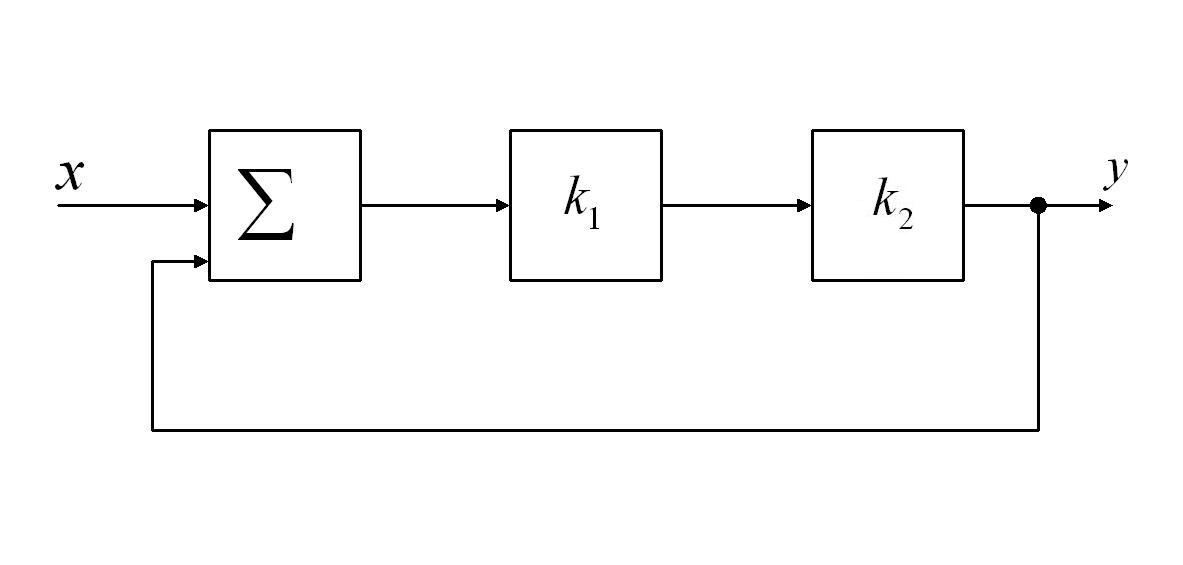
Рис. 3.1 Система регулирования

Математической моделью системы является дифференциальной уравнение

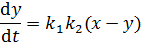
или

Характеристики состояния системы

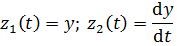
Функционирование системы заключается в изменении характеристик состояния во времени. В некоторых случаях характеристики состояния могут определяться в виде явных функций от параметров системы, входных сигналов, начальных условий и времени. В других случаях модель представляет собой систему уравнений относительно характеристик состоянии системы и выходных сигналов. При этом параметры входят в коэффициенты уравнений, а входные сигналы – в их правые части.

Вид математической модели определяется природой реального объекта, и теми задачами, для решения которых строится модель, а также требуемой точностью их решений. Поэтому необходимо исследование полученной модели с целью определения области ее наиболее эффективного использования при решении инженерной задачи и установления границ изменения переменных, в которых она справедлива.

Рассмотрим в качестве примера построение модели Солнечной системы.

Наблюдение за звездным небом начались еще в глубокой древности. Первичный анализ этих наблюдений позволил выделить планеты из всего разнообразия небесных светил. Следовательно, первым шагом было выявление объекта исследования. Другим шагом стало выявление закономерности движения планет, то есть «аксиом» гипотетической модели. Сначала была создана модель Птолемея (II ст. до н.э.) – геоцентрическая модель. В ней Солнце и планеты двигались вокруг Земли. Эти движения описывались с помощью правил (формул), но по мере накопления результатов наблюдения они постоянно усложнялись.

М.Коперник в 1543 году предложил принципиально новую модель Солнечной системы – гелиоцентрическую. В ней все планеты вращаются вокруг Солнца.

Однако эта модель еще не было математической, поскольку не было параметров модели (скоростей движения планет, параметров орбит и т.д.).

В XVII в. Кеплер сформулировал законы движения планет. Они описывали кинематику движения каждой планеты в отдельности, не касаясь причин, вызывающих это движение.

И.Ньютон во 2-й половине XVII века предложил динамическую модель Солнечной системы. Она базировалась на открытом им законе всемирного тяготения. Динамическая модель Ньютона согласовалась с кинематической моделью Кеплера.

Однако в 40-х годах XIX ст. результаты динамической модели стали противоречить накопленным результатам наблюдений. Например, движение планеты Уран отклонялось от теоретически вычисленного движения на модели. Это позволило Леверье в 1846 г. предсказать новую планету – Нептун, которая влияет на движение планеты Уран. Позже в том месте, на которое указал Леверье, действительно была открыта планета Нептун.

Подобным образом была предсказана и позже открыта в 1930 г. планета Плутон. Одновременно в открытием новых планет, совершенствовалась и модель Солнечной системы.