Топологические уравнения.

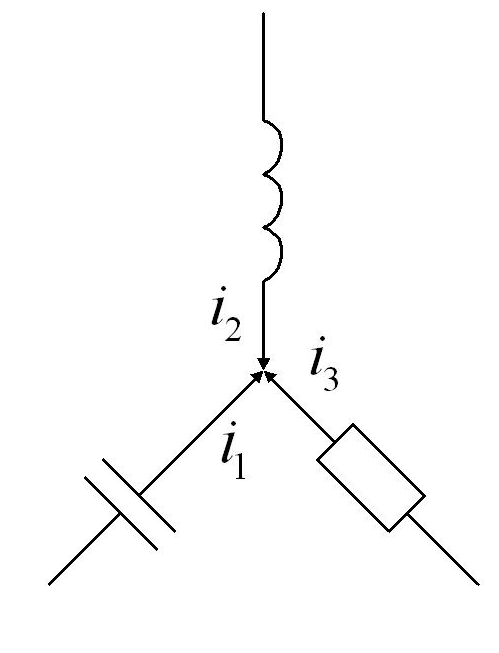
Эти уравнения характеризуют способ соединения ветвей, не отражая их содержимого. Топологические уравнения обычно строятся на законах Кирхгофа. Как известно, есть закон Кирхгофа для токов (ЗКТ) и закон Кирхгофа для напряжений (ЗКН). ЗКТ гласит: алгебраическая сумма токов связанных с узлом, равна нулю. На рис. 3.3 (а) показан узел.

(а) (б)

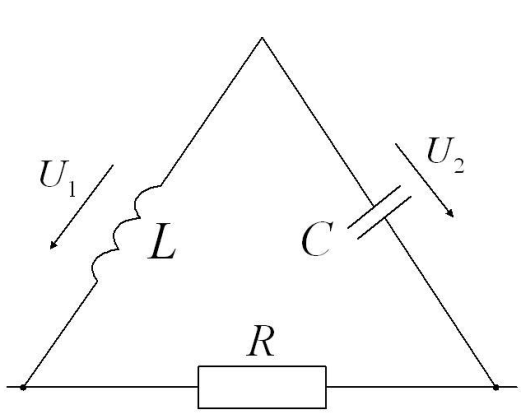
Рис 3.3 Электрический узел (а) и замкнутый контур (б)

Для него ЗКТ записывается так 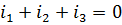. ЗКН звучит так, алгебраическая сумма напряжений ветвей в замкнутом контуре равна нулю. Для контура, изображенного на рис. 3.3 (б) ЗКН записывают так: 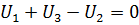. Эти уравнения не содержат сведений о том, какие типы элементов включены в ветви и каковы их параметры. Известно, что если в схеме n-узлов, то по ЗКТ можно составить (n-1) независимых уравнений. Для составления уравнений по ЗКН в схеме должны быть найдены независимые замкнутые контуры, т.е. такие контура, в каждом из которых имеется хотя бы одна ветвь, не входящая во все другие контура. Поиск независимых контуров для цепи со сложной конфигурацией (топологией) представляет собой относительно большую трудность. Чтобы получить топологические уравнения каждую ветвь электрической цепи представляют линией, которая соединяет соответствующие узлы. Получается так называемый граф цепи. Пример приведен на рис. 3.4, рис. 3.5.

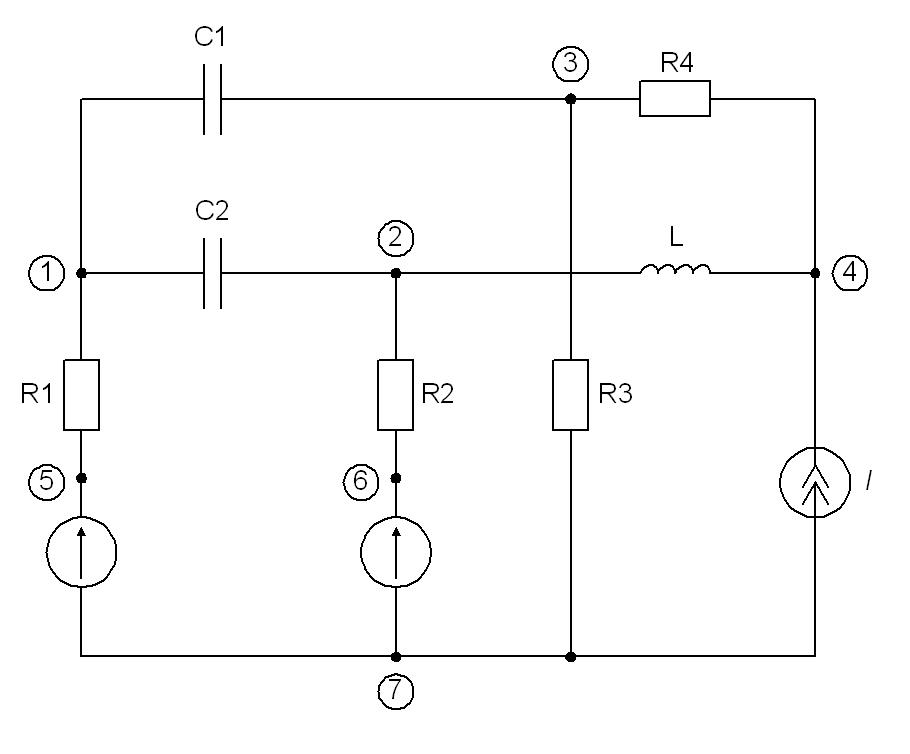
Рис. 3.4 Пример электрической цепи

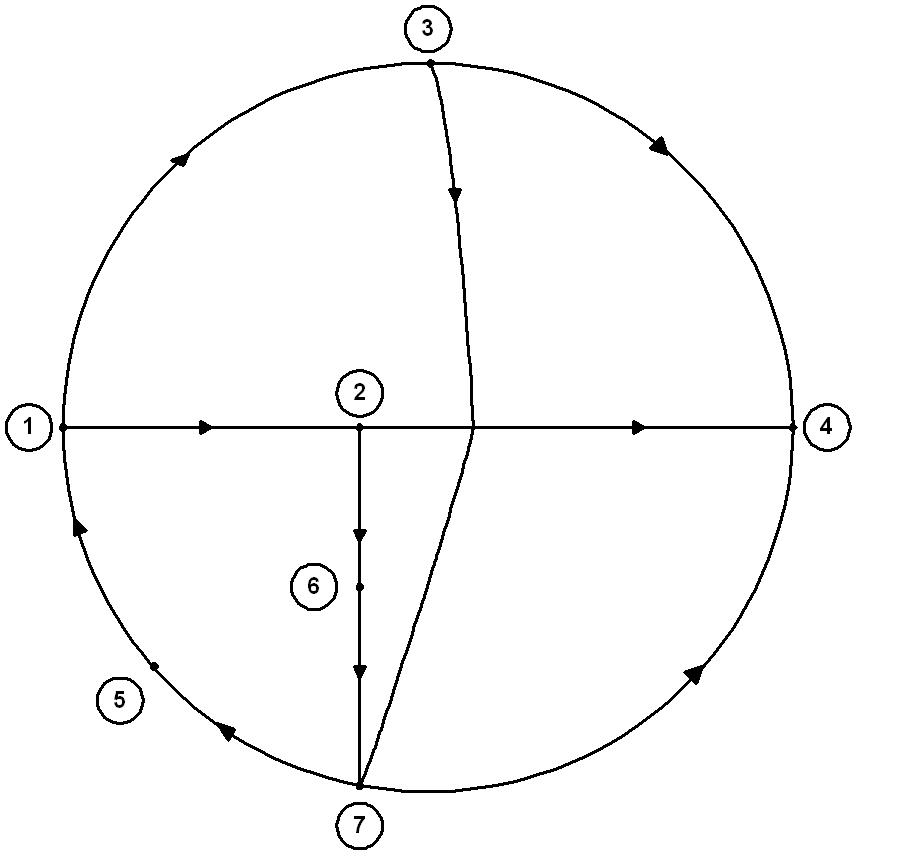
Рис. 3.5 Граф цепи

Выбор положительного направления тока и напряжения на графе делается произвольно. При этом полагается, что выбранное положительное направление тока одновременно является и положительным направлением напряжения.