Докажем, что MN является высотой в равнобедренном треугольнике КМР, т. е.

<91011 12 13 14 15 >

1. D КМР – равнобедренный (МК=МР);

2. MN – медиана (КN =NР);

3. MN – высота (MN^КР).

D АМN=D ВМN=D СМN=D DМN ( как прямоугольные треугольники по двум катетам)

1. 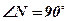, так как MN^АС, MN^ВD;

2. MN – общий катет;

3. АN = ВN = СN = DN по построению.

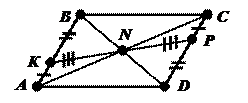Из равенства треугольников следует, что АМ = ВМ = СМ = DМ.

D АВМ = D СDМ (по трём сторонам)

1. АD=ВС по построению;

2. АМ = СМ;

3. ВМ = DМ.

Из равенства треугольников следует, что .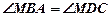

D ВМК = D DМР (по двум сторонам и углу между ними)

1. ВК= DР (по свойству параллелограмма);

2. ВМ=DМ;

3. ( как ).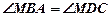

Из равенства треугольников следует, что МК = МР. Значит D КМР – равнобедренный.

По свойству параллелограмма NК = NР, следовательно, MN является медианой в равнобедренном треугольнике. А, значит, MN – высота.

Вывод: Чтобы доказать, что данная прямая перпендикулярна данной плоскости, надо в этой плоскости найти две пересекающиеся прямые, которым данная прямая перпендикулярна.

Упражнения:

1. Сторона АВ правильного треугольника АВС лежит в плоскости a . Может ли быть перпендикулярна к этой плоскости:

A) ВС,

<91011 12 13 14 15 >

Дата добавления: 2017-05-02; просмотров: 1917;