Следовательно, предположение неверно, а верно то, что требовалось доказать. Через данную точку можно провести только одну прямую, перпендикулярную к данной плоскости.
Как проверить, перпендикулярна ли данная прямая к данной плоскости? Этот вопрос имеет практическое значение, например, при установке мачт, колонн зданий, которые нужно поставить прямо, т. е. перпендикулярно к той плоскости, на которую они ставятся. Оказывается, для этого нет необходимости проверять перпендикулярность данной прямой к любой прямой этой плоскости, как о том говорится в определении.
Докажем признак перпендикулярности прямой и плоскости.
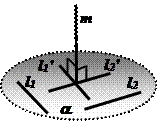
Теорема: Если прямая перпендикулярна к двум пересекающимся прямым, принадлежащим плоскости, то она перпендикулярна к этой плоскости.
Дано: 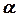 ,
, 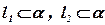 ,
, 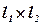 ,
, 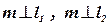 .
.
Доказать: 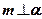 .
.
Доказательство:
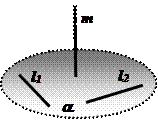 Чтобы доказать, что
Чтобы доказать, что 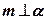 , докажем, что прямая т перпендикулярна произвольной прямой l, принадлежащей плоскости
, докажем, что прямая т перпендикулярна произвольной прямой l, принадлежащей плоскости 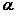 .
.
Пусть 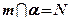 ,
, 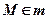 .
. 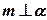 , если
, если 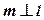 , т. е.
, т. е. 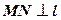
Дополнительные построения:
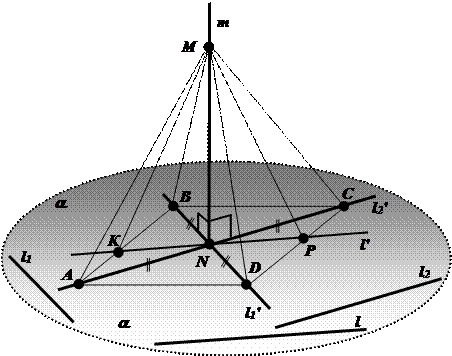 Через точку N, принадлежащую плоскости a , проведём прямые
Через точку N, принадлежащую плоскости a , проведём прямые 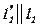 и
и 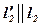 ,
, 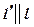 .
.
На прямых 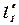 и
и 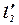 от точки N отложим отрезки
от точки N отложим отрезки 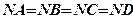 . Соединяя последовательно точки
. Соединяя последовательно точки 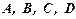 , получим прямоугольник АВСD (АС = ВD).
, получим прямоугольник АВСD (АС = ВD).
Прямая 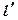 пересекает стороны АВ и СD соответственно в точках К и Р .
пересекает стороны АВ и СD соответственно в точках К и Р .
Точку М соединяем с точками 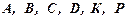 .
.
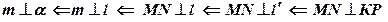
Дата добавления: 2017-05-02; просмотров: 2409;











