ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ

<9 10 111213 14 15 >

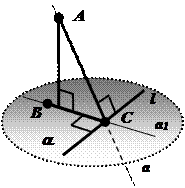Теорема: Для того чтобы прямая, принадлежащая плоскости, была перпендикулярна наклонной к этой плоскости, необходимо и достаточно, чтобы она была перпендикулярна проекции этой наклонной.

Необходимое условие:

Дано: 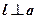Доказать: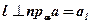

Доказательство:

; ; ;

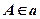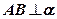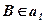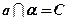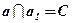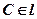Через точки А, В, С проходит единственная плоскость АВС. По признаку перпендикулярности прямой и плоскости прямая l перпендикулярна плоскости АВС:

1) 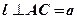по условию теоремы;

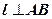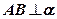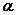2) , так как , а значит, она перпендикулярна любой прямой, принадлежащей плоскости .

, значит, прямая l перпендикулярна любой прямой, принадлежащей плоскости 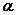. Следовательно, 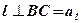, т. е. .

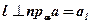Достаточное условие:

Дано: 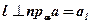Доказать: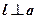

Доказательство:

По признаку перпендикулярности прямой и плоскости прямая l перпендикулярна плоскости АВС:

1. 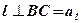по условию теоремы;

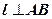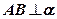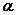2. , так как , а значит, перпендикулярна любой прямой, принадлежащей плоскости .

, значит, прямая l перпендикулярна любой прямой, принадлежащей плоскости 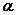. Следовательно, 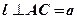, т. е. .

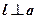Вывод: Чтобы доказать, что наклонная перпендикулярна прямой, лежащей в плоскости, надо показать, что её проекция перпендикулярна этой прямой.

Упражнения:

<9 10 111213 14 15 >

Дата добавления: 2017-05-02; просмотров: 2315;