Методы синтеза систем с обратной связью

Метод динамического программирования позволило обосновать задачу синтеза оптимальных линейных систем по интегральному квадратичному критерию.

Рассматривается объект управления, возмущенное движение которого описывается в первом приближении уравнением

(5.1)

где A и B – числовые матрицы размерности n´n и n´m.

Требуется найти матрицу C^T размерности m´n уравнения регуляторов

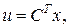(3.23)

такую, чтобы на асимптотически устойчивых движениях системы (5.1) и (5.2), при начальных условиях x⁰ минимизировался функционал

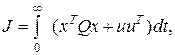(5,4)

где Q – заданная положительно-определенная симметричная матрица размерности n´n (x^TQx > 0 для всех x, это обозначается далее в виде Q > 0).

Для решения этой задачи об оптимальной стабилизации применяется метод динамического программирования. Структуру решения уравнения Беллмана ищут в виде квадратичной формы x^TPx. Матрица P определяется из матричного алгебраического уравнения Риккати

(5.5)

где P – симметричная матрица размеров n´n.

Этот метод называется также аналитическим конструированием регуляторов на основе метода динамического программирования и состоит из трех этапов:

1. Решение системы нелинейных алгебраических уравнений Риккати.

2. Выделение из всего множества этих решений матрицы P⁰ > 0;

3. Вычисление искомой матрицы коэффициентов регулятора по формуле

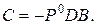(3.26)

Для численного решения матричного алгебраического уравнения Риккати разработаны методы решения Репина-Треьякова, Ньютона-Рафсона, диагонализации [2]. В системе MATLAB для решения этого уравнения имеется функция careпакета Control System Toolbox [Лазарев].

Литература

1. . Аттетков А.В., Галкин С.В., Зарубин В.С. Методы оптимизации. Учеб. для вузов. – М., Изд-во МГТУ им. Н.Э. Баумана, 2003. – 440 с.

2. Методы классической и современной теории автоматического управления. Учебник в 5 томах./Под ред.К.А. Пупкова и Н.Д. Егупова. - М., Изд-во МГТУ им. Н.Э. Баумана. 2004.

Т.4.Теория оптимизации систем автоматического управления, 2004.-744с.

3. Пантелеев А.В. Методы оптимизации в примерах и задачах. Учебное пособие для вузов. – М., Высш. шк., 2002. – 544с.

4. Ванько В.И.,Вариационное исчисление и оптимальное управление: Учебник для вузов. Под ред. В.С.Зарубина, А.П. Крищенко. – 2-е издание. - М., Изд-во МГТУ им. Н.Э. Баумана, 2002. – 488 с.

5. Дьяконов В.П. MATLAB 6/6.1/6.5 + Simulink 4/5. Основы применения. Полное руководство пользователя. – М: Солон-Пресс. 2002.- 768 с.

6. Дьяконов В., Круглов В. MATLAB. Анализ, идентификация и моделирование систем. Специальный справочник. – Спб.: Питер, 2002. – 448с.