Отображение структуры в форме отношений

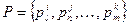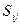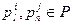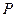В множестве кинематических пар может быть определена закономерность, устанавливающая между ними отношение . Можно выделить некоторые пары из указав, какая из них является первой, какая второй и т.д. Если кинематические пары 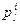и 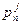соединены между собой связью, то есть являются смежными, то между ними можно считать, что существуют отношения.

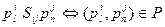(1)

Если кинематические пары 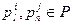не соединены, то есть не смежны, то они не находятся в отношениях

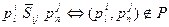(2)

Для кинематической цепи, представляющей совокупность кинематических пар, соединенных между собой связями, имеет место отношение

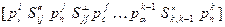(3)

При этом верхний индекс при 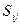указывает, как соединены кинематические пары или ориентированы их оси в пространстве: 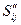- параллельно; 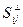- перпендикулярно; 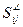- под углом; 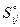- коллинеарно; 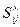- скрещиваются и т.д.

Структура манипулятора (рис. 4) может быть описана:

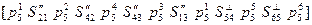. (4)

где 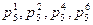- вращательные кинематические пары пятого класса,

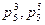- поступательные кинематические пары пятого класса, 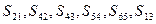- взаимные связи,

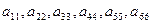- параметрические веса кинематических пар, 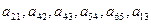- параметрические веса взаимных связей.

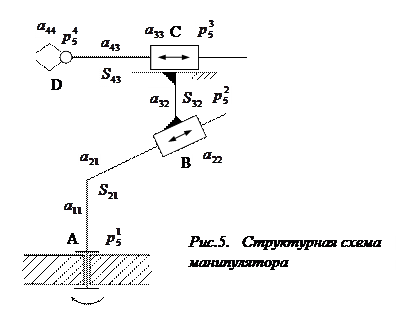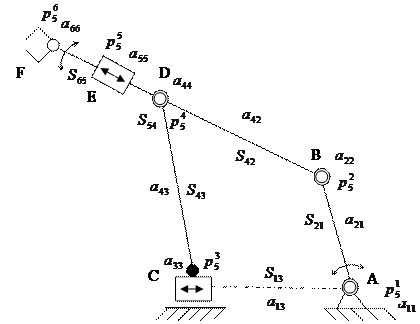
Для механизма изображенного на рис. 5 структура описывается как:

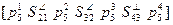(5)

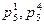- вращательные кинемати­ческие пары пятого класса,

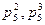- поступательные кинема­тические пары пятого класса,

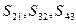- взаимные связи,

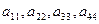- параметрические веса кинематических пар,

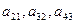- параметрические веса взаимных связей.

В (4) пара 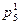встречается два раза, что свидетельствует о наличии замкнутого контура в структуре механизма. Таким образом, по выражениям отношений можно идентифицировать тип структуры.

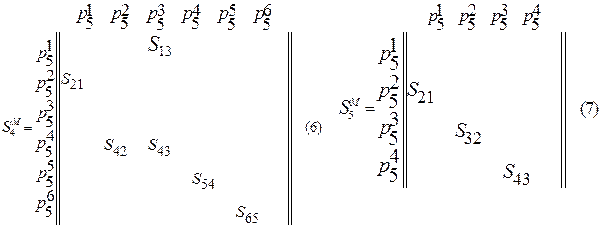Взаимнооднозначное представление отношений 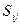к 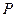можно установить матрицей отношений 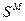, составленной в соответствии со следующими правилом: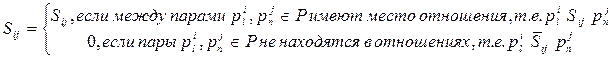

Матрицы отношений для ориентированных структур манипуляторов, изображенных на рис.4 и рис. 5:

Отношение 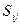носят бинарный характер и указывают для каждых двух кинематических пар: имеют место отношения или нет. Бинарные отношения в множестве кинематических пар, входящих в структуру манипулятора, образуют булеву алгебру. Все законы булевой алгебры применимы к алгебре отношений. Используя тождественные отношения и формулы булевой алгебры, можно находить новые структуры манипуляторов, эквивалентные исходной.