Структурная значимость кинематической пары

Для прогнозирования возможных последствий частичной потери подвижности пары необходимо знание величины критерия значимости пары. Структурную значимость кинематической пары 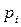в первом приближении можно оценить влиянием ее числа степеней свободы на общую подвижность манипулятора. Более точно и объективно значимость пары оценивается ее рангом .

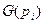Рангом 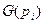называется величина, характеризующая структурную и функциональную значимость пары в кинематической цепи манипулятора. Для нахождения рангов пар используют комплексную матрицу смежности С_к, в которой диагональными элементами 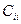являются степени свободы кинематических пар 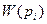, а не диагональные 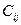отображают локальные степени пар .

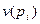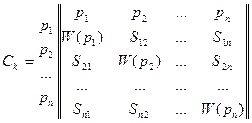
Ранг кинематической пары равен сумме членов строки матрицы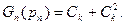

Более представительно характеризуют значимость удельные значения рангов пар q(p_i):

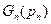где - сумма элементов строки кинематической матрицы , соответствующая данной кинематической паре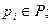

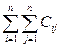- сумма всех элементов матрицы.

В качестве примера определим структурную значимость пар манипулятора (рис. 7).

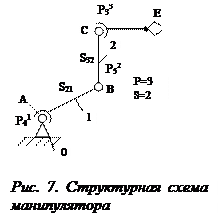1. Устанавливаем, что цепь манипулятора описывается структурным множеством P(P, S)=P (3, 2) и выражением отношений 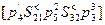. В цепи содержатся пары 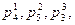имеющие локальные степени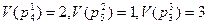

2. Составляем матрицу смежности кинематической цепи.

3. Определяем значение рангов.

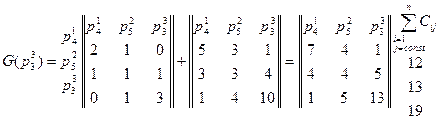
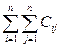=44

4. Вычисляем удельные значения рангов кинематических пар

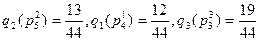
Анализируя полученные значения q_i(p_i) следует отметить, что их величины соответствуют действительной значимости кинематических пар в функционировании манипулятора. Наибольший ранг имеет пара 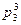, что обусловливается не только числом её степеней свободы, но и положением в кинематической цепи. В случае выхода из строя пар 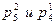манипулятор потеряет возможность перемещаться в направлении определенных осей координат, но будет обладать всеми возможными движениями захвата и тем самым выполнять функциональное назначение.