Интегрирующее звено

Простейший пример интегрирующего звена – ванна, в которую набирается вода. Входной сигнал – это поток воды через кран, выход системы – уровень воды в ванне. При поступлении воды уровень растет, система «накапливает» (интегрирует) входной сигнал.

Интегрирующее звено описывается уравнением

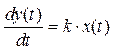, (5)

которому соответствует передаточная функция 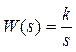. Решение уравнения (5) дает

.

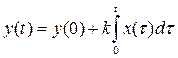Используя это решение для единичного скачка (x(t) = 1 при t ≥ 0) при нулевых начальных условиях (y(0) = 0), получаем линейно возрастающую переходную характеристику

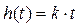. (6)

Для того, чтобы найти импульсную характеристику, вспомним, что интеграл от дельта-функции на любом интервале, включающем t = 0 , равен 1. Поэтому ω(t) = k (при t ≥ 0).

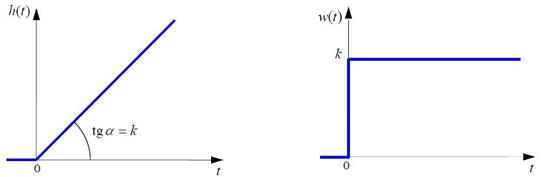
Рисунок 4.5 - Графики переходной и весовой функций интегрирующего звена

Частотная характеристика интегрирующего звена определяется формулой 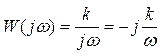. Можно показать, что его логарифмическая амплитудная частотная характеристика – это прямая с наклоном − 20 дБ/дек. На низких частотах усиление максимально, теоретически на частоте ω = 0 оно равно бесконечности. Высокие частоты, наоборот, подавляются интегратором.

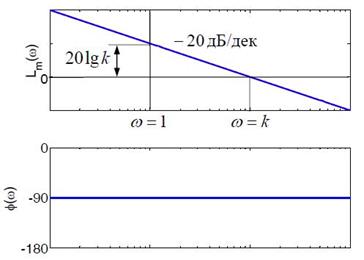
Рисунок 4.6 – Асимптотические ЛАЧХ интегрирующего звена

На частоте ω = 1 значение ЛАЧХ равно 20lgk, а при ω = k ЛАЧХ обращается в нуль, поскольку 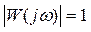. Фазовая характеристика φ(ω) = −90° – говорит о постоянном сдвиге фазы на всех частотах.