Дифференцирующие звенья

Дифференцирующее звено дает на выходе производную входного сигнала. Уравнение идеального дифференцирующего звена

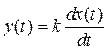, (7)

его операторная запись 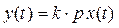, а передаточная функция .

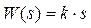Известно, что производная единичного ступенчатого сигнала 1(t) в точке t = 0 – это дельта-функция δ(t). Поэтому переходная и весовая функции дифференцирующего звена

.

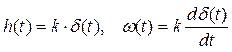Это физически нереализуемые функции, так как дельта-функцию и ее производную, имеющие бесконечные значения, невозможно получить на реальном устройстве. Поэтому идеальное дифференцирующее относится к физически нереализуемым звеньям.

Логарифмическая амплитудная частотная характеристика дифференцирующего звена – прямая с наклоном 20 дБ/дек, пересекающая ось абсцисс 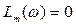на частоте 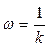. При ω = 1 ЛАЧХ равна 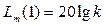. Дифференцирующее звено подавляет низкие частоты (производная от постоянного сигнала равна нулю) и бесконечно усиливает высокочастотные сигналы, что требует бесконечной энергии и невозможно в физически реализуемых системах.

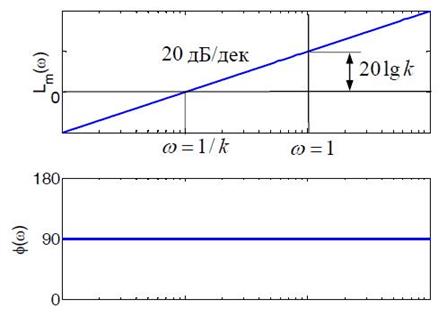
Рисунок 4.7 – Асимптотические ЛАЧХ дифференцирующего звена

Фазовая характеристика не зависит от частоты, звено дает положительный сдвиг фазы на 90°. Действительно, при дифференцировании сигнала 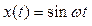получаем

.

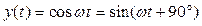Дифференцирующее звено реагирует не на изменение самой входной величины, а на изменение ее производной, то есть на тенденцию развития событий. Поэтому говорят, что дифференцирующее звено обладает упреждающим, прогнозирующим действием. С его помощью можно ускорить реакцию системы.

В технике не могут использоваться физически нереализуемые звенья. Поэтому важно рассмотреть аналогичное звено, которое выполняет дифференцирования низкочастотных сигналов и одновременно имеет ограниченное усиление на высоких частотах. Инерционное дифференцирующее звено описывается уравнением

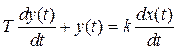(8)

и имеет передаточную функцию 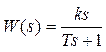. Фактически это последовательное соединение идеального дифференцирующего и апериодического звеньев.

Апериодическое звено добавляет инерционность: обладая свойствами фильтра низких частот, оно ограничивает усиление на высоких частотах. Поскольку передаточная функция имеет равные степени числителя и знаменателя, на высоких частотах (выше сопрягающей частоты 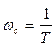) ЛАЧХ имеет нулевой наклон, поэтому неограниченного роста коэффициента усиления не происходит. Одновременно теряется точность дифференцирования, так как фазовая характеристика изменяется от 90° до нуля.

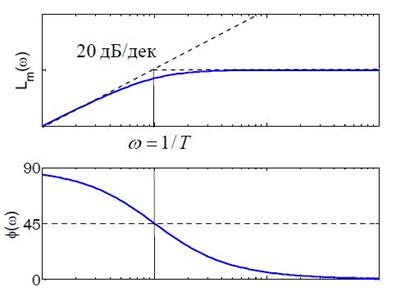
Рисунок 4.8 – Асимптотические ЛАЧХ инерционного дифференцирующего звена

Запаздывание

Представим себе трубу, через которую вентилятор прокачивает воздух. В начале трубы установлен нагреватель, а температура воздуха измеряется датчиком в точке А.

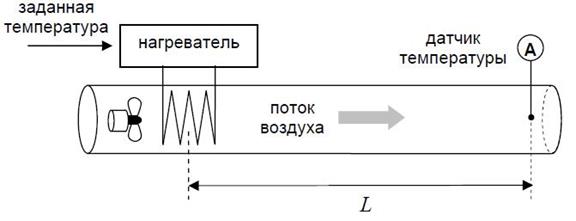
Рисунок 4.9 – Динамическое звено запаздывания

Очевидно, что при изменении температуры воздуха датчик обнаружит это не сразу, а через время 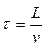, где L – длина трубы (в метрах), а v – скорость потока воздуха (в м/с). В этом случае говорят, что в системе есть транспортное запаздываниена величину τ (в секундах).

Другой распространенный пример – вычислительное запаздывание в компьютере. Так называется время, которое необходимо для расчета нового управляющего сигнала после получения всех исходных данных.

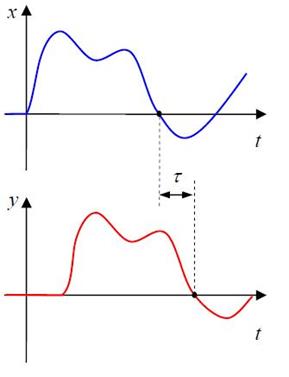
Рисунок 4.10 – Сдвиг сигнала в системе управления

Запаздывание в системе просто сдвигает сигнал вправо на временной оси, не меняя его формы. Математически это можно записать в виде

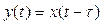. (9)

Изображение сигнала на выходе звена запаздывания вычисляется по теореме о смещении аргумента для преобразования Лапласа

.

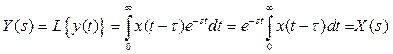поэтому передаточная функция звена чистого запаздывания равна .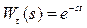

Очевидно, что при гармоническом входном сигнале запаздывание не изменяет амплитуду, но вносит дополнительный отрицательный сдвиг фазы. Частотная характеристика этого звена имеет вид 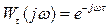. По общим формулам находим

.

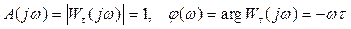Таким образом, фазовая частотная характеристика звена запаздывания – линейная функция частоты ω, чем больше частота, тем больше фазовый сдвиг.