Колебательное звено

Колебательное звено – это звено второго порядка с передаточной функцией вида

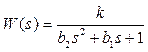, (3)

знаменатель которой имеет комплексно-сопряженные корни (то есть, 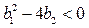). Как известно из теории дифференциальных уравнений, свободное движение такой системы содержит гармонические составляющие (синус, косинус), что дает колебания выхода при изменении входного сигнала.

Несложно представить передаточную функцию колебательного звена в форме

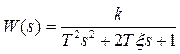, (4)

где k – коэффициент, T – постоянная времени (в секундах), ξ – параметр затухания (0 < ξ < 1). Постоянная времени определяет инерционность объекта, чем она больше, тем медленнее изменяется выход при изменении входа. Чем больше ξ, тем быстрее затухают колебания.

При ξ = 0 в уравнении получается консервативное звено, которое дает незатухающие колебания на выходе. Если ξ ≥ 1, модель представляет апериодическое звено второго порядка, то есть последовательное соединение двух апериодических звеньев.

Колебательное звено относится к позиционным звеньям, его статический коэффициент усиления равен W(0) = k.

Переходная и импульсная характеристики отличаются выраженной колебательностью, особенно при малых значениях параметра затухания ξ. На следующих двух графиках синие линии соответствуют ξ = 0,5, а красные – ξ = 0,25 .

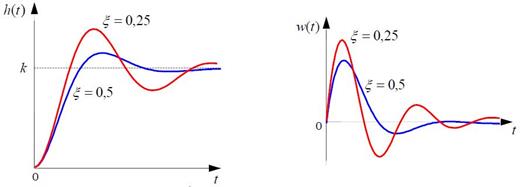
Рисунок 4.3 – Графики переходной и весовой функций колебательного звена

Асимптотическая ЛАЧХ этого звена образована двумя прямыми, которые пересекаются на сопрягающей частоте 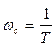. На низких частотах она имеет нулевой наклон (так как звено позиционное), причем в этой области .

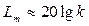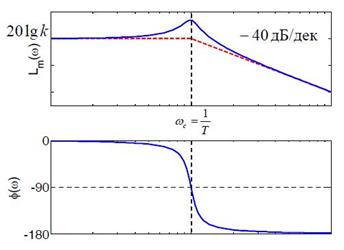
Рисунок 4.4 – Асимптотическая ЛАЧХ колебательного звена

На высоких частотах наклон ЛАЧХ равен − 40 дБ/дек, так как степень знаменателя передаточной функции на два больше степени ее числителя. Фазовая характеристика меняется от 0 до −180° , причем на сопрягающей частоте ω_с она равна − 90° .

При значениях ξ < 0,5 ЛАЧХ имеет так называемый «горб» в районе сопрягающей частоты, причем его высота увеличивается с уменьшением ξ. Это означает, что при частоте входного сигнала, равной ω_с, наблюдается резонанс, то есть частота возмущения совпадает с частотой собственных колебаний системы.

В предельном случае при ξ = 0 (консервативное звено) ЛАЧХ терпит разрыв (обращается в бесконечность) на частоте ω_с, при таком входе амплитуда колебаний неограниченно растет и на практике объект разрушается.