Дифференциальные уравнения

МОДЕЛИ ЛИНЕЙНЫХ ОБЪЕКТОВ

Составляя модель объекта на основании физических законов, мы чаще всего получаем систему дифференциальных уравнений первого и второго порядка.

Для примера покажем, как построить модель двигателя постоянного тока, используя законы механики и электротехники. Вход этого объекта – напряжение якоря u(t) (в вольтах), выход – угол поворота вала θ(t) (в радианах).

Сначала вспомним некоторые «житейские» знания об электродвигателях. Вал двигателя начинает вращаться, когда приложено напряжение питания. Если напряжение не меняется, угловая скорость вращения ω(t) (в радианах в секунду) остается постоянной, при этом угол θ(t) равномерно увеличивается.

Чем больше напряжение, тем быстрее вращается вал. Если зажать вал рукой (или подключить нагрузку, например, заставить двигатель вращать турбину), скорость вращения постепенно уменьшается до нового значения, при котором вращающий момент двигателя будет равен моменту сопротивления (нагрузки). Пока эти моменты равны, скорость вращения остается постоянной и ее производная равна нулю.

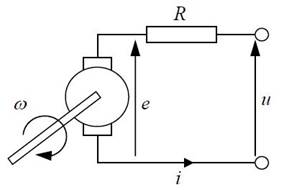
Рисунок 3.1 – Вращение вала ДПТ

Теперь переведем эти рассуждения на строгий язык математики. Угловая скорость вращения ω(t) вычисляется как производная от угла поворота вала θ(t), то есть 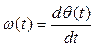. Соответственно, угол θ(t) – это интеграл от угловой скорости. В механике уравнение вращательного движения обычно записывают в виде

,

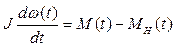где M(t) – вращающий момент (измеряется в H·м), M_H(t) – момент нагрузки (возмущение, также в H·м). Буквой J обозначен суммарный момент инерции якоря и нагрузки (в кг·м²). Величина момента инерции говорит о том, насколько легко «разогнать» двигатель (чем больше момент инерции, тем сложнее «разогнать»).

Перейдем к электротехнике. В нашем случае момент M(t) – это электромагнитный момент двигателя, который вычисляется по формуле

,

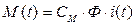где C_М – коэффициент, Φ – магнитный поток, создаваемый обмоткой возбуждения (измеряется в веберах); i(t) – ток якоря (в амперах), который может быть найден из уравнения

,

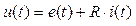где e(t) – электродвижущая сила (ЭДС) якоря (в вольтах) и R – сопротивление якорной цепи (в омах). В свою очередь, ЭДС рассчитывается через магнитный поток и частоту вращения

,

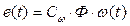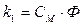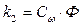где C_ω – коэффициент. Вводя новые постоянные и , можно записать модель двигателя в виде системы уравнений

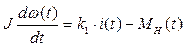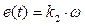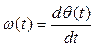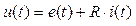, , , . (1)

Модель (1) описывает связи реальных сигналов в системе, ее внутреннее устройство.

Часто нам достаточно знать, как будет реагировать объект на заданный входной сигнал (управление). При этом его внутреннее устройство нас не очень интересует, то есть мы рассматриваем объект в качестве «черного ящика». Подставив второе уравнение из системы (1) в четвертое, найдем i(t) и подставим в первое уравнение. Переходя к переменной θ(t) , получаем

,

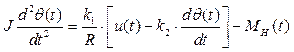или, перенося все члены, зависящие от θ(t) , в левую часть равенства

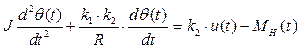. (2)

Это дифференциальное уравнение второго порядка, связывающее вход u(t) и нагрузку M_H(t) с выходом θ(t). В сравнении с системой (1), все внутренние сигналы исходной модели (e(t) и i(t)) были исключены из уравнений. Поэтому уравнение (2) называется уравнением «вход-выход».

Порядком модели называют порядок соответствующего дифференциального уравнения. В данном случае мы получили модель второго порядка.

В этом разделе на простом примере мы посмотрели, как на основе физических законов строятся математические модели объектов управления. Как правило, они представляют собой дифференциальные уравнения.