Модели в пространстве состояний

Для того, чтобы было легче исследовать модель объекта, желательно привести ее к некоторому стандартному виду, для которого уже есть готовые общие решения. Таким «стандартом» в теории управления считается система дифференциальных уравнений первого порядка, которая называется нормальной формой Коши.

Рассмотрим снова модель электродвигателя, считая, что M_H(t)=0 (нагрузки нет). Вспомнив, что 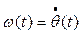, можно записать (2) в виде системы

.

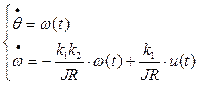Эта система дифференциальных уравнений первого порядка быть записана в матричной форме

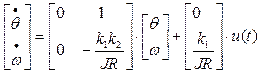. (3)

Значения θ(t) и ω(t) определяют состояние двигателя в момент времени t . Это значит, что зная их значения в некоторый момент времени t₀ и входной сигнал u(t) при всех t ≥ t₀ можно рассчитать поведение объекта для любого последующего момента. При этом предыдущие значения θ(t) , ω(t) и u(t) (при t < t ₀) не играют никакой роли. Поэтому θ(t) и ω(t) называются переменными состояния, а вектор 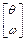- вектором состояния.

В теории управления принято обозначать вектор состояния через x(t), вход объекта (сигнал управления) – через u(t) . Тогда модель (3) может быть записана в виде

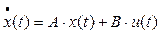, (4)

где 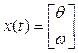, , 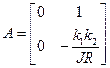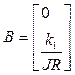. Модель (4) связывает вход u(t) и вектор состояния x(t) , поэтому она называется моделью вход-состояние.

Полная модель объекта в пространстве состояний содержит еще одно уравнение – уравнение выхода, которое показывает, как формируется выход объекта y(t)

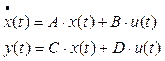, (5)

Эта модель называется моделью вход-состояние-выход. Выходная координата для двигателя постоянного тока – это угол поворота вала

,

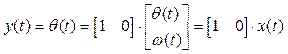так что 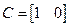и D=0. Если же в качестве выхода принять угловую скорость, то .

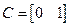С помощью модели (5), изменяя матрицы C и D, можно принять за выход любую линейную комбинацию переменных состояния и входа. Во многих практических задачах выход – это одна или несколько переменных состояния, которые мы можем измерить.

Поскольку момент инерции J , сопротивление якоря R и коэффициенты k₁ и k₂ не зависят от времени, матрицы A, B, C и D в модели (5) – постоянные. Такие объекты называются стационарными, в отличие от нестационарных объектов, параметры которых изменяются во времени.

Запись моделей в единой форме (5) позволяет отвлечься от смысла переменных состояния и исследовать системы разной природы стандартными методами, которые хорошо разработаны и реализованы в современных компьютерных программах.

Пример, как уравнения вида (5) могут быть решены и чем удобна именно такая форма записи. Предположим, что известны начальные условия, то есть вектор состояния x(0) при t = 0. Знание x(0) и входа u(t) при всех t > 0 дает возможность однозначно определить дальнейшее поведение этого объекта.

Первое уравнение в (5) позволяет найти производную, то есть, скорость изменения вектора состояния x(t) в любой момент времени. Будем считать, что при 0 ≤ t ≤ Δt , где Δt – малый интервал времени, эта производная не меняется. Тогда значение вектора состояния при t = Δt приближенно определяется формулой

,

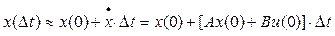то есть, его можно легко вычислить. Зная x(Δt) и сигнал управления u(Δt) , находим выход системы в тот же момент

.

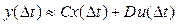Таким образом, можно (приближенно) рассчитать выход системы при всех t > 0 . Конечно, точность будет тем выше, чем меньше Δt , однако объем вычислений при этом также увеличится. Этот метод приближенного решения дифференциальных уравнения называется методом Эйлера. Так как не делается никаких предположений о постоянных матрицах A , B , C и D, его (как и другие, более совершенные методы) можно использовать без изменений для решения любых уравнений вида (5).

Переходная функция

Один из методов построения моделей «вход-выход» – определение реакции объекта на некоторый стандартный сигнал. Один из простейших сигналов – так называемый «единичный скачок» («единичный ступенчатый сигнал»), то есть мгновенное изменение входного сигнала с 0 до 1 в момент t = 0 . Формально этот сигнал определяется так

.

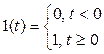Реакция объекта на единичный скачок называется переходной функциейи обозначается h(t)

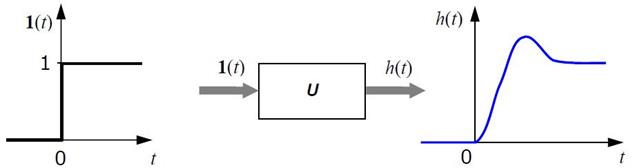
Рисунок 3.2 – График переходной функции h(t)

При этом предполагается, что объект в начальный момент находится в состоянии покоя, то есть, имеет нулевые начальные условия. Это значит, что все его переменные состояния равны нулю и внутренняя энергия также нулевая.

Если начальные условия ненулевые, то для построения сигнала выхода при любом входе нужно использовать дифференциальные уравнения объекта или модель в пространстве состояний. Это значит, что переходная характеристика дает меньше информации, чем исходные уравнения.

Пусть модель объекта задана дифференциальным уравнением первого порядка

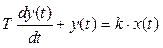, (6)

где k – безразмерный коэффициент, а T – некоторая постоянная, которая имеет размерность времени (измеряется в секундах). Найдем переходную характеристику этого звена. Решая уравнение (6) при x(t) = 1 (t > 0), получаем

,

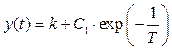где постоянная C₁ должна определяться из начальных условий. Поскольку нас интересует переходная характеристика, начальные условия считаем нулевыми, то есть y(0) = 0, что дает C₁ = −k и поэтому

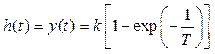. (7)

На рисунке показаны переходные характеристики (7) при различных значениях параметра T, который называется постоянной временизвена

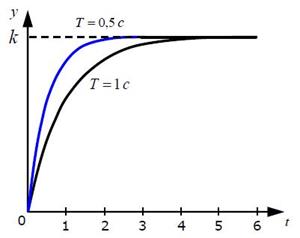
Рисунок 3.3 – Переходные характеристики

Видно, что при увеличении T выход y медленнее достигает установившегося значения, равного k, то есть постоянная времени характеризует инерционность звена (6). Чем больше постоянная времени, чем медленнее реагирует объект на управление и тем больше усилий нужно для того, чтобы перевести его в новое состояние.

Заметим, что ступенчатый сигнал легко получить на практике, поэтому переходную характеристику можно снять экспериментально.