Передаточная функция

Выходной сигнал системы можно представить как результат действия некоторого оператора на ее вход. Для линейных моделей такой оператор можно записать следующим образом.

Пусть модель объекта задана линейным дифференциальным уравнением второго порядка, связывающим вход x(t) и выход y(t)

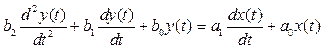, (8)

где a_i (i = 0,1) и b_i (i = 0,1,2)– постоянные.

Введем оператор дифференцирования 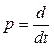, который действует на сигнал x(t) по правилу .

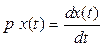Теперь запишем производные сигналов x(t) и y(t) по времени в операторной форме

.

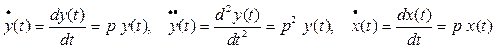Подставляя эти выражения в (8), получим

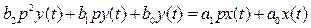. (9)

Можно формально вынести за скобки y(t) в левой части равенства (9) и x(t) в правой части

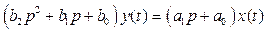. (10)

Левая часть (10) означает, что оператор 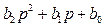действует на сигнал y(t), а в правой части оператор 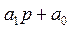действует на сигнал x(t) . «Разделив» (условно, конечно) обе части (10) на оператор 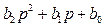, связь выхода и входа можно записать в виде

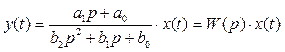, (11)

где запись W(p)·x(t) означает не умножение, а действие сложного оператора

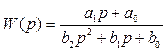(12)

на сигнал x(t). Иначе говоря, формула y(t)=W(p)·x(t) – это не что иное, как символическая запись уравнения (8), которую удобно использовать.

Функция W(p) называется передаточной функциейобъекта, который описывается уравнением (8). Она полностью описывает связи между выходом и входом объекта при нулевых начальных условиях, но не учитывает его внутреннее устройство.

Часто передаточной функцией называют функцию W(λ), которая получается из (12) в результате замены оператора p на некоторую независимую переменную λ. Эта фукнция представляет собой отношение двух полиномов (многочленов) от λ .

Передаточная функция W(λ) называется правильной, если степень ее числителя не больше, чем степень знаменателя; строго правильной, если степень числителя меньше степени знаменателя; неправильной, если степень числителя больше, чем степень знаменателя. Например, функция 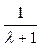– строго правильная и одновременно правильная; 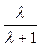– правильная, но не строго правильная (иногда такие функции называют биправильными), а 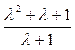– неправильная.

Нулямипередаточной функции называются корни ее числителя, а полюсами– корни знаменателя. Например, функция 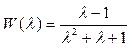имеет нуль в точке λ = 1 и два полюса в точках λ = −1 и λ = −2 .