Методы глобального освещения

Математическое моделирование освещения, при котором используются упрощенные модели – прямое освещение от конечного числа точечных источников без учета переотражений, получило название локального освещения (local illumination). Моделирование освещения, при котором достаточно точно воспроизводятся реальные характеристики ОП и оптические свойства отражающих/пропускающих свет поверхностей, учитываются процессы переотражения света, затенение источников света и экранирование поверхностей, а также учитывается текстура поверхности и изменение цветности излучения при взаимодействии с отражающими/пропускающими поверхностями называется глобальным освещением (global illumination). Методы глобального освещения впервые появились в среде компьютерной графики.

В глобальном освещении используется следующая терминология:

Сцена – совокупность пространственно расположенных геометрических объектов, источников света и камеры. Описание сцены обычно включает в себя различные свойства её элементов, такие как оптические характеристики отражающих и преломляющих свет поверхностей объектов, текстуру поверхностей, цветовые характеристики излучения ИС и колориметрические свойства поверхностей, участвующих в перераспределении света.

Камера – условный наблюдатель (фотоаппарат или глаз человека), помещенный в сцену и характеризуемый точкой расположения в сцене, направлением наблюдения и полем охвата сцены.

Рендеринг – процесс воспроизведения компьютером трехмерного изображения сцены при её визуализации.

Методология глобального освещения включает в себя построение яркостной модели сцены, а также построение трехмерных геометрических моделей объектов и их преобразование при перемещении камеры, затенение источников света, экранирование одних объектов другими, построение текстур, учет цвета и др.

С фотометрической точки зрения построение изображения сцены сводится к нахождению распределения поля яркости, видимого в направлении камеры. Основным уравнением глобального освещения является уравнение визуализации, которое связывает яркость точки отражающей поверхности сцены с яркостью окружающего пространства.

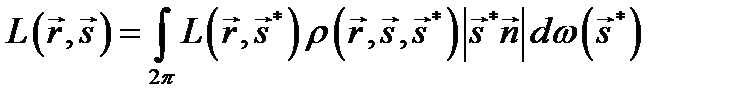
где 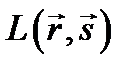- яркость в точке A(r) поверхности объекта сцены в направлении камеры, определяемом вектором s. 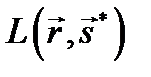- яркость, видимая из точки A в направлении источника света (вектора s*). 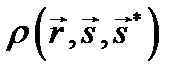- функция двунаправленного распределения отражения (bidirectional reflection distribution function) BDRF - коэффициент яркости при направленном освещении зависящий от точки A(r), но не от одного направления визирования, а и от направления освещения или падения излучения. 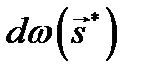- элементарный телесный угол относительно вектора падающего от источника света луча s*.

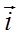
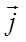
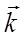
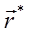
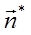
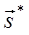
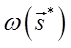
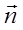
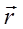
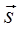
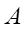
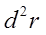
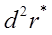
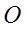
Функция 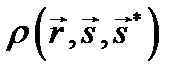характеризует направленность отражающих свойств поверхности и определяется как отношение яркости элемента поверхности, содержащего точку A(r), в направлении s, к освещенности этого элемента, обусловленной световым потоком, упавшим на этот элемент в телесном угле 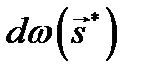в направлении s*:

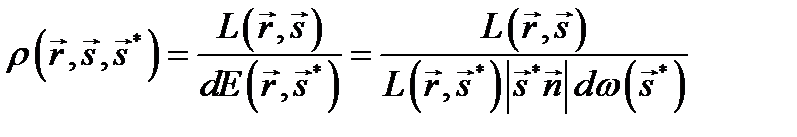
По аналогии с отражающими поверхностями для прозрачных поверхностей используется функция двунаправленного распределения пропускания (bidirectional transmittance distribution function) BTDF - 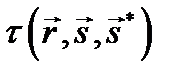. В случае и отражения и пропускания используется обобщенная функция двунаправленного распределения рассеяния (bidirectional scattering distribution function) BSDF - :

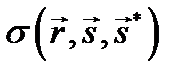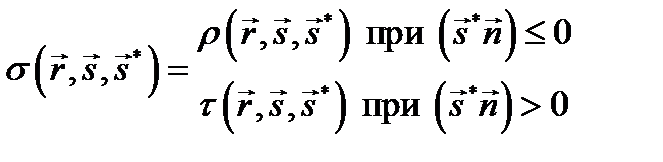
Если точка A находится на самой излучающей поверхности, то в уравнение визуализации необходимо добавить слагаемое, определяющее яркость этой поверхности за счет собственного излучения:

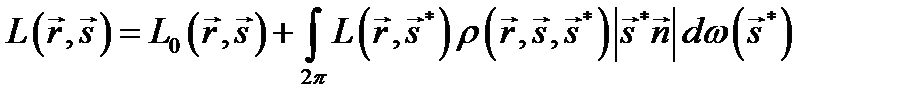
Это уравнение обычно представляют в другой форме, переходя от интегрирования по телесному углу к интегрированию по поверхности сцены, для чего выражают элемент телесного угла через элемент поверхности излучателя:

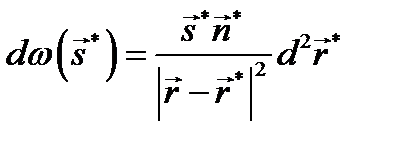
Также в уравнение вводят функцию видимости

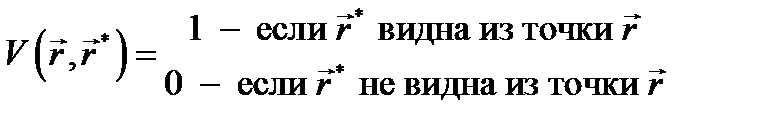
Тогда уравнение визуализации примет вид:

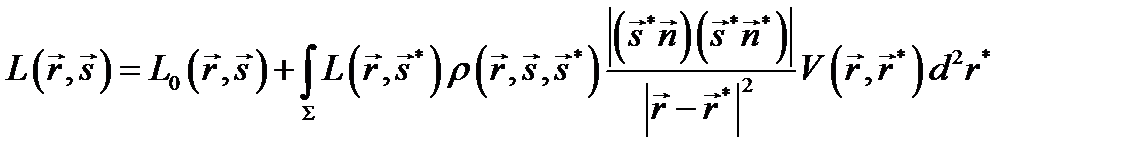
где Σ – суммарная поверхность всех элементов сцены

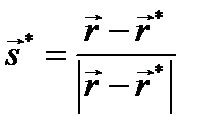
Также для упрощения вводят предположение о ламбертовском характере отражения.

Для решения практических задач уравнение визуализации в такой форме непригодно из-за невозможности получить аналитическое решение, поэтому были разработаны специальные численные методы.