Основы теории гидравлического моделирования

Виды подобия и второй закон Ньютона.

При изучении гидравлических явлений прибегают к изучению их на моделях. В основе моделирования гидравлических явлений лежат законы подобия. Их три вида: геометрическое, кинематическое, динамическое (механическое).

Геометрическое подобие- это подобие форм двух тел или объектов, для обеспечения которого необходимо, чтобы отношения между всеми линейными размерами модели и в натуре были одинаковыми.

Кинематическое подобие- это подобие движения. Кинематическое подобие обеспечивается при равенстве отношений скоростей всех соответствующих частиц жидкости на модели и в натуре при соблюдении геометрического подобия траекторий движения на обоих объектах.

Динамическое или механическое подобие - это подобие масс и сил. Для обеспечения динамического подобия необходимо добиться равенства отношений между силами, приложенными и соответствующим частицам жидкости на модели и в натуре.

Общая теория подобия базируется на втором законе Ньютона (закон движения). Для того, чтобы на модели сообщить частице жидкости массой 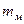ускорение 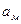, к ней необходимо приложить силу

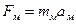. (216)

Зная, что масса равна произведению плотности на объем, можно записать

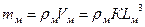(217)

где		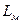- один из характерных размеров модели;
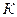
		- коэффициент пропорциональности, зависящий от геометрической формы рассматриваемой частицы жидкости.

Ускорение:

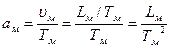(218)

где		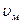- скорость частиц жидкости на модели;
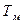
		- отрезок времени, за который частица жидкости приобрела ускорение .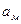

Подставив все это в (216), получим

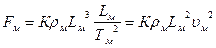. (219)

Аналогичное выражение для силы 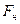, приложенной к частице жидкости в натуре, будет иметь вид:

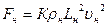(220)

Отношение:

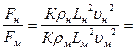
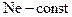(221)

Это закон подобия Ньютона, формулируется так:

в механически подобных процессах соотношение между двумя соответствующими силами действующими в натуре и на модели, равно постоянному числу Nе, называемому числом Ньютона.

Но движущаяся жидкость находится под воздействием различных сил, отличающихся друг от друга своей физической сущностью. Когда на жидкость действуют силы различной физической природы (и трения, и поверхностное натяжение), не удается добиться равенства числа Nе для всех сил. Поэтому при моделировании стремятся выделить главную силу, определяющую характер движения в качественном и количественном отношениях.

В инженерной практике чаще всего приходится встречаться с гидравлическими явлениями, основную роль в которых играют силы тяжести или силы внутреннего трения жидкости. Существует два основных закона гидравлического моделирования: Фруда и Рейнольдса.

Закон Фруда

На законе Фруда основано моделирование гидравлических явлений, преобладающее значение в которых имеют силы тяжести, например при изучении движения жидкости в открытых руслах, истечении жидкости через большие отверстия и водосливы. Эти силы, приложенные к модели и в натуре, можно выразить так

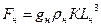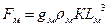и (222)

отношение:

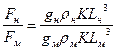(223)

Приравняв правые части (221) и (223) имеем:

,

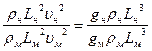Учитывая, что 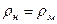, запишем:

; или 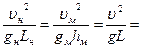Fr. (224)

Это закон Фруда: в механически подобных процессах, протекающих под влиянием силы тяжести, должны быть одинаковы числа Фруда.

.

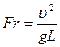Число Фруда Fr - величина пропорциональная отношению сил инерции к силам тяжести.

Для проектирования явлений на моделях необходимо иметь масштабные зависимости, устанавливающие связь между различными геометрическими, кинематическими и динамическими характеристиками натурального и модельного потока жидкости:

- масштаб длин

-

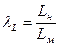; (225)

- масштаб площадей

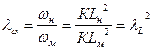; (226)

- масштаб объемов

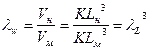; (227)

- масштаб уклонов

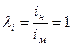(одинаковы) (228)

- масштаб времени

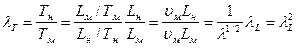; (229)

- масштаб расходов

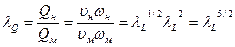; (230)

- масштаб сил

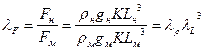; (231)

- масштаб давлений

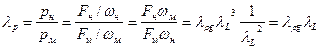(232)

где 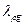- масштаб объемного веса.

Закон Рейнольдса

На законе Рейнольдса основано моделирование явлений, основную роль, в которых играют силы внутреннего трения жидкости.

Силы внутреннего трения, приложенные к соответствующим площадям на модели и в натуре, можно выразить

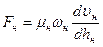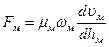и (233)

где 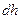- текущий размер.

Отношение

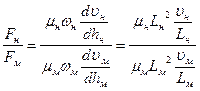(234)

где 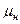, 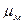μ_н и μ_м - динамические коэффициенты вязкости.

Приравняв число Nе (Ньютона) и (234), будем иметь:

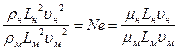; (235)

Зная, что 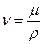, после сокращения получим

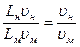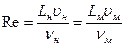или (236)

Это закон Рейнольдса: в механически подобных процессах, протекающих под влиянием внутренних сил трения жидкости, должны быть одинаковы числа Рейнольдса 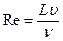, вычисленные для соответствующих элементов натуры и модели.

Масштабы геометрических характеристик при моделировании по закону Рейнольдса принимаются такими же, как и при моделировании по Фруду.

- масштаб скоростей

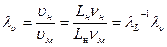, (237)

где 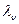- масштаб кинематической вязкости.

- масштаб расходов

. (238)

- масштаб сил

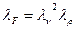(239)

- масштаб давлений

(240)