Гидравлические струи
Гидравлическая струя - конечный поток жидкости, не ограниченный твердыми стенками. Бывают затопленными и незатопленными. Струя, вытекающая в однородную жидкость, называется затопленной; в атмосферу - незатопленной (брандспойт, для разработки грунта).
Незатопленная струя, вытекающая из насадка с цилиндрическим отверстием в атмосферу, имеет следующую структуру по длине: 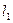 - компактная,
- компактная, 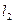 - раздробленная,
- раздробленная, 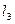 - распыленная часть струи.
- распыленная часть струи.

Рис. 56. Схема струи
В компактной части струи обеспечивается сплошность потока, струя имеет правильную цилиндрическую форму. В раздробленной 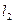 обнаруживается нарушение сплошности потока, струя разрывается на крупные части. Распыленная часть струи
обнаруживается нарушение сплошности потока, струя разрывается на крупные части. Распыленная часть струи 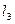 состоит из множества отдельных капель, в которые превращается весь поток.
состоит из множества отдельных капель, в которые превращается весь поток.
Для разработки грунтов, добычи угля, воздействия на лопатки активной гидравлической турбины требуется струя с хорошо развитой компактной частью 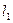 .
.
Для определения осевой скорости струи в пределах её компактной части существует формула Н. П. Гавырина:
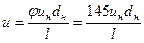 (180)
(180)
| где | 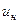
| - скорость струи при выходе из насадка, 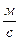 ; ;
|
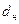
| - диаметр струи при выходе из насадка, 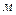 ; ;
| |
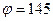 - коэффициент. - коэффициент.
|
Для определения дальности полета струи пользуются экспериментальной формулой Н. П. Гавырина
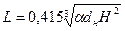 (181)
(181)
| где | 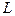
| - дальность полета, м; |
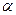
| - угол вылета струи, град; | |
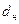
| - диаметр насадка, мм; | |
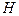
| - напор, при выходе из насадка, м. |
Расчет турбин
Рассмотрим воздействие гидравлической струи на неподвижную преграду. Предположим, что струя вытекает из сопла со средней скоростью и встречает на своем пути неподвижную вертикальную стенку.
Если вертикальная стенка плоская, то струя ударяясь о нее, растекается во все стороны. Для того, чтобы струя растекалась при встрече лишь по двум направлениям, сделаем в вертикальной стене направляющий желоб, попав в который струя после удара разделится на верхнюю и нижнюю части.
Пусть струя имеет в сечении 1 - 1 площадь живого сечения 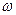 и среднюю скорость
и среднюю скорость 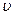 . Расход
. Расход 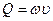 до встречи со стенкой.
до встречи со стенкой.
При встрече со стенкой струя разделится на две части: 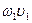 и
и 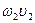 . Очевидно, что
. Очевидно, что 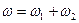 принимаем
принимаем 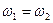 и
и 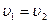 .
.
Выделим отсек струи 1- 2 - 3. За время 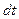 этот отсек переместится в новое положение 1¢ - 2¢ - 3¢.
этот отсек переместится в новое положение 1¢ - 2¢ - 3¢.
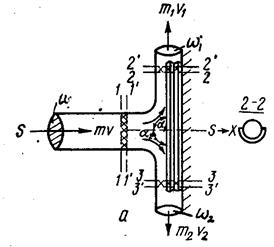
Рис. 57. Схема разделения струи.
Применим к движению отсека теорему количества движения, которая звучит: изменение проекции количества движения на заданную ось за время 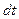 равно сумме проекций импульсов приложенных внешних сил на ту же ось за то же время. Примем за ось S - S. Тогда на основании этой теоремы:
равно сумме проекций импульсов приложенных внешних сил на ту же ось за то же время. Примем за ось S - S. Тогда на основании этой теоремы:
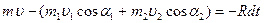 (182)
(182)
| где | 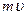
| - количество движения объема жидкости, заключенной между сечениями 1 - 1 и 1¢ - 1¢; |
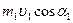 , , 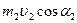 - количество движения объемов жидкости, заключенных между сечениями 2 - 2; 2¢ - 2¢; 3¢ - 3¢; - количество движения объемов жидкости, заключенных между сечениями 2 - 2; 2¢ - 2¢; 3¢ - 3¢;
| ||
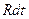
| - импульс силы реакции стенки; | |
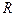
| - реакция неподвижной вертикальной стенки, (по закону Ньютона, действие равно противодействию, следовательно 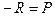 ). ).
|
Из рисунка видно, что 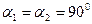 , а
, а 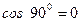 . И уравнение примет вид:
. И уравнение примет вид:
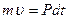 (183)
(183)
где 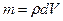 ;
;
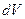 - элементарный объем струи между сечениями 1 - 1 и 1¢ - 1¢, т.е.
- элементарный объем струи между сечениями 1 - 1 и 1¢ - 1¢, т.е. 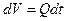 ,
,
тогда уравнение (183) будет таким:
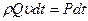 (184)
(184)
откуда сила воздействия струи на вертикальную стенку будет:
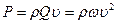 , (185)
, (185)
Если стенка находится под некоторым углом к струе, то
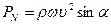 (186)
(186)
Мощность струи, действующей на подвижную преграду (лопатку турбины), определим так: пусть плоская лопатка движется со скоростью vл, тогда
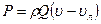 ,
,
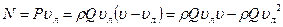 ,
,
где 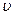 - скорость струи,
- скорость струи, 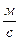 ;
;
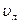 - скорость лопатки,
- скорость лопатки, 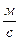 .
.
Максимальное значение мощности можно получить при 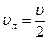 :
:
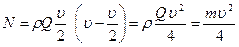 (187)
(187)
Т.е. максимальная теоретическая мощность турбины с плоскими лопатками равна половине полной кинетической энергии струи. В действительности потери энергии составляют 40-45%. Если применить криволинейные лопатки в виде ковшей, то при 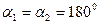 и
и 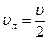 , сила давления на полусферические поверхности равна
, сила давления на полусферические поверхности равна
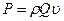
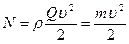
Дата добавления: 2017-05-02; просмотров: 2696;











