Интерполяционный полином в форме Лагранжа

Пусть на отрезке [a, b] задана одномерная сетка

h_x = {x_i / x_i = x_{i – 1} + h_i, h_i > 0, i = 1, 2, 3, …, n; x₀ = a, x_n = b},

в узлах x_i которой заданы y_i = f(x_i), i = 0, 1, 2, …, n – соответствующие значения функции f(x).

Будем искать интерполяционный полином

P_n(x) = a₀ + a₁x + a₂x² + … + a_nxⁿ (3.2.1)

в виде

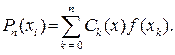(3.2.2)

Для выполнения условий интерполяции по узлам сетки h_x

P_n(x_i) = y_i, i = 0, 1, 2, …, n (3.2.3)

достаточно, чтобы

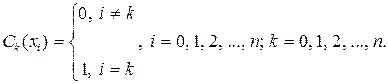(3.2.4)

Действительно, если функции C_k(x), k = 0, 1, 2, …, n удовлетворяют условиям (3.2.4), то и полином P_n(x) в виде (3.2.2) будет удовлетворять условиям интерполяции (3.2.3).

Так как интерполяционный полином P_n(x) является полиномом степени n, то с учетом (3.2.2) функции C_k(x), k = 0, 1, 2, .., n можно задавать полиномами той же степени.

С учетом условий (3.2.4) будем определять C_k(x), k = 0, 1, 2, …, n
в виде

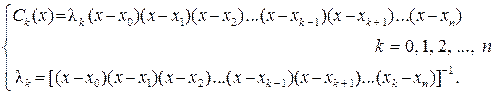(3.2.5)

Очевидно, что при таком задании функций C_k(x), k = 0, 1, 2, …, n
условия (3.2.4) будут выполнены.

Подставив (3.2.5) в (3.2.2), получим следующее выражение для P_n(x), x Î (a, b):

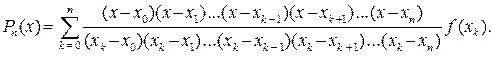(3.2.6)

Введем в рассмотрение функцию w(x):

w(x) = (x – x₀)(x – x₁)(x – x₂)(x – x₃) … (x – x_n). (3.2.7)

Очевидно, что w(x) является полиномом степени n + 1. Продифференцировав w(x), найдем выражение для w¢(x) в узлах сетки h_x:

w¢(x_k) = (x_k – x₀)(x_k – x₁) … (x_k – x_{k – 1})(x_k – x_{k + 1}) … (x_k – x_n),

k = 0, 1, 2, …, n. (3.2.8)

Подставив (3.2.7) и (3.2.8) в (3.2.6), перепишем выражение для интерполяционного полинома в виде

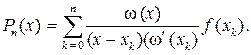3.2.9)

Полином в виде (3.2.9) называют интерполяционным полиномом в форме Лагранжа.

Существенно, что рассмотренный подход к построению интерполяционного полинома не требует решения системы линейных уравнений (3.1.3). При интерполяции таблично заданной функции с использованием интерполяционного полинома в форме Лагранжа удобно пользоваться матрицей вида

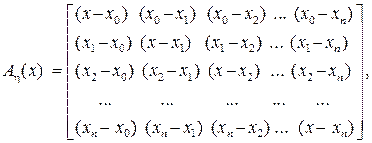(3.2.10)

где x_k, k = 0, 1, 2, …, n – узлы сетки h_x.

Произведение элементов, находящихся на главной диагонали матрицы А_h(x), позволяет вычислить значение w(x) в точке x, а произведение элементов k-й строки (исключая диагональный элемент) этой матрицы – значения w¢(x_k), k = 0, 1, 2, …, n. В результате достаточно легко найти значения коэффициентов

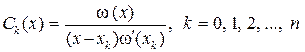(3.2.11)

для интерполяционного полинома в форме Лагранжа.

Процесс интерполяции таблично заданной на отрезке [a, b] функции в заданную точку x^* Î (a, b) с помощью интерполяционного полинома в форме Лагранжа можно представить в виде следующего алгоритма:

0. На отрезке [a, b] задать одномерную сетку

h_x = {x_i / x_i = x_{i – 1} + h_i, h_i > 0, i = 1, 2, 3, …, n; x₀ = a, x_n = b}

и значения y_i = f(x_i) в узлах сетки x_i, i = 0, 1, 2, …, n.

Задать x^* Î (a, b).

1. Положить k: = 0, S: = 0.

2. Вычислить элементы матрицы А_h(x) для заданной сетки h_x и x = x^*.

3. Вычислить значение w(x^*) как произведение диагональных элементов матрицы А_h(x).

4. Вычислить значение w¢(x_k), как произведение всех элементов k-й строки матрицы А_h(x), за исключением диагонального элемента.

Рассчитать значение коэффициента

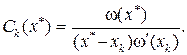
5. Рассчитать r = C_k(x^*) f(x_k).

6. Положить S: = S + r.

7. Если k = n, перейти к выполнению п. 9.

8. Положить k: = k +1, перейти к выполнению п. 4.

9. Процесс завершен. Полученное значение S и есть результат интерполяции табличных данных в точку x^*.

Для визуальной оценки качества интерполирования желательно вычислить значения интерполяционного полинома P_n(x) с достаточно малым шагом по переменной x и построить его график на отрезке [a, b], что позволит наглядно сопоставить его с табличными данными.

В заключение отметим ряд характерных особенностей интерполирования данных с помощью интерполяционного полинома в форме Лагранжа.

1. Интерполяционный полином в форме Лагранжа удобно использовать, когда есть необходимость интерполяции в точку x^* различных функций, таблично заданных на одной и той же сетке. В этом случае коэффициенты C_k(x^*) достаточно вычислить лишь один раз при интерполировании первой функции. В связи с этим целесообразно запоминать расчетные значения коэффициентов C_k(x^*) в процессе вычислений.

2. Как уже было сказано ранее, не рекомендуется использовать интерполяционные полиномы выше 6-го порядка: в этом случае при их построении может быть использовано в совокупности не более семи узлов сетки, находящихся на оси Ох с обеих сторон от точки x^* Î (a, b).

3. Имеет место следующая оценка точности полиномиальной интерполяции:

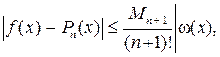(3.2.12)

где M_{n + 1} – верхняя граница значения модуля (n + 1)-й производной функции f(x) на отрезке [a, b].

В соответствии с (3.2.12) погрешность интерполяции будет равна нулю, если интерполируемая функция представляет собой полином, степень которого не превышает n.

4. Интерполяционный полином в форме Лагранжа часто оказывается удобным для проведения различных теоретических исследований в области вычислительной математики.