Для решения системы линейных уравнений

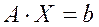(1)

умножим обе части уравнения на матрицу 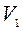, получим эквивалентную (1) систему, матрица которой 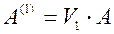содержит нули в первом столбце ниже главной диагонали. Затем умножаем обе части уравнения на 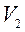и так далее: 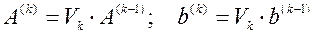. В результате умножения матричного уравнения (1) на цепочку матриц

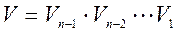
приводим А к верхнему треугольному виду (для этого потребуется 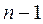шагов). Перед выполнением k–го шага матрица 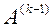имеет вид:

.

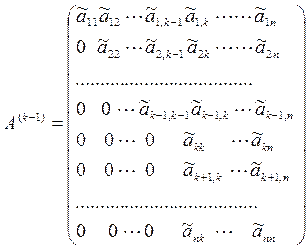Поскольку на k–ом шаге обрабатывается только часть матрицы, а именно элементы 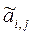, , 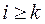, 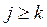то для экономии памяти ЭВМ можно на каждом шаге уменьшать размерность матрицы 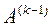и вектора 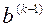и строить матрицу отражения 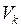размерности .

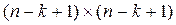Для удобства вычислений используют расширенную матрицу (A÷b), где (n +1)-й столбец – это столбец свободных членов 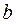(см. п 4.1.1)

Для k = 0 считаем 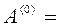(A÷b).

Для k = 1 строим матрицу 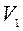, где 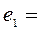(1; 0; ...; 0)^T, 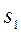– первый столбец матрицы 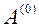, производим умножение 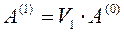. Затем исключаем из 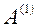1–ю строку и 1–й столбец (получаем 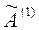размерности ).

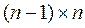Для k = 2 строим матрицу 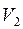, где 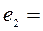(1; ...; 0)^T, 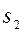– первый столбец матрицы 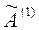. (Отметим, что размерность векторов 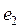и 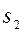уменьшилась на единицу по сравнению с размерностью векторов 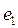и 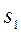) Производим умножение 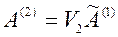и вновь уменьшаем размерность 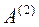на единицу, исключая из нее 1–ю строку и 1–й столбец.

Продолжаем процесс для k = 3, 4, ... Для 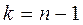строим матрицу 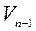размерности 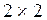, и осуществляем последнее умножение: 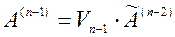. В итоге получим систему с верхней треугольной матрицей. Обратный ход осуществляется так же, как в других методах.

Задача

Решить систему из п.4.5.1 с использованием матриц отражения.

Решение. Прямой ход.

k = 0. 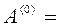(A÷b) = .

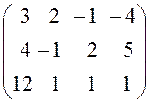k = 1. 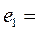(1;0;0)^Т; 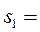(3;4;12)^T; ;

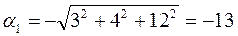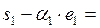(16; 4; 12); 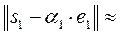20,396;

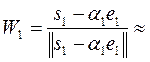(0,784; 0,196; 0,588).

Матрица отражения: .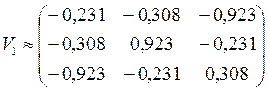

Результат первого шага:

.

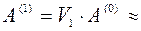
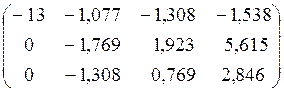Уменьшаем размерность: .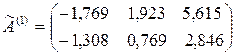

k = 2. 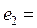(1; 0)^T; 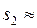(–1,769; –1,308)^T; 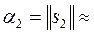2,200;

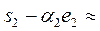(–3,969; –1,308); 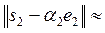4,179;

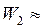(–0,950; –0,313); .

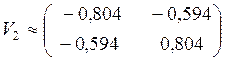Результат второго шага:

.

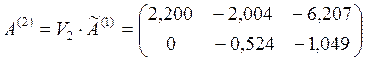Результат прямого хода:

.

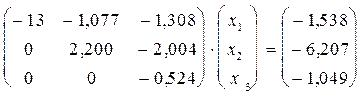Обратный ход:

; ;

.

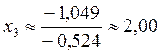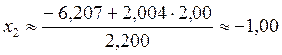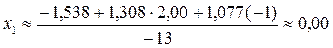Ответ: ; ; .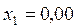

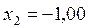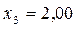Для контроля при построении матриц вращения и отражения можно проверять выполнение равенств, справедливых для всех ортогональных матриц : Q^T×Q = E или Q×Q^T = E, где Е – единичная матрица.

Методы решения систем с использованием ортогональных преобразований обладают устойчивостью к ошибкам округления, легко программируются и нечувствительны к провалам главных миноров, в отличие от некоторых других схем (например, Гаусса). Однако, эти методы требуют большего числа арифметических операций (примерно вдвое больше).

Литература

[1], гл. III, работы №2, № 4–6.

[2], часть 1 гл. IV, §6, № 444–448, 450-451; §7, № 457.

[4], т. II, гл. VI, §2.1; §3.

[5], гл. II, §2.11.

[6], гл. III, §2,4,5,6.

[7], гл. V, §1.2, 1.5, 1.6.

Конспект лекций.