Метод наискорейшего спуска

Дана система уравнений

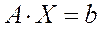,(1)

где 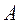-симметричная положительно определенная матрица (невырожденная). Решение этой системы может быть найдено при помощи итерационного процесса:

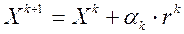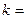, 0, 1, ... . (2)

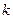Здесь – вектор невязки на –ом шаге:

, (3)

а число 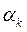, регулирующее при каждом 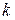длину шага в направлении 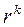от точки 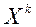, находится таким образом, чтобы обеспечить минимум функции 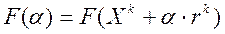. Такое продвижение от точки 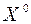к , затем от 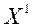к 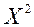и т.д. приводит в случае сходимости процесса к 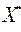- точке минимума функции 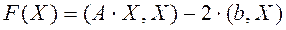. Нетрудно показать, что 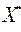является в этом случае и решением системы (1).

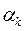Для рассматриваемого случая (симметричной положительно определенной матрицы ) коэффициенты находятся по формулам

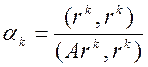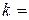, 0, 1, ... . (4)

Если матрица А не является симметричной, то от системы (1) можно перейти к систем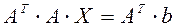е , где 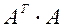– симметричная матрица.

Формулы (2), (3), (4) – расчетные формулы метода наискорейшего спуска. В качестве 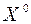можно взять любой вектор. Критерий остановки расчетов: .

В рассматриваемом случае симметричной положительно определенной матрицы итерационный процесс сходится со скоростью геометрической прогрессии. Условие сходимости: 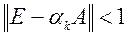, (5).

Существуют различные модификации этого метода. В частности, число 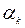можно взять постоянным для всех , из условия сходимости .

Задача

Решить методом наискорейшего спуска систему уравнений:

.

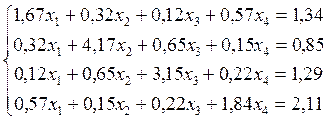Точность = 0,01.

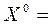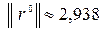Решение. Возьмем начальное приближение (0; 0; 0; 0)^T. Тогда (1,34; 0,85; 1,29; 2,11), . Дальнейшие расчеты приведены в таблице.

k
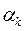
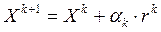
	2,938	0,320	(0,429; 0,272; 0,413; 0,675)T
	1,014	0,275	(0,457; 0,055; 0,306; 0,810)T
	0,333	0,344	(0,478; 0,108; 0,326; 0,908)T
	0,152	0,309	(0,463; 0,077; 0,306; 0,932)T
	0,074	0,385	(0,453; 0,093; 0,312; 0,952)T
	0,047	0,318	(0,444; 0,084; 0,306; 0,958)T
	0,025	0,387	(0,440; 0,090; 0,309; 0,963)T
	0,016	0,318	(0,437; 0,086; 0,307; 0,965)T
	0,008

Поскольку 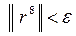, вычисления прекращаем.

Ответ: 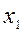= 0,44; 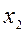= 0,09; 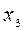= 0,31; = 0,97.