Систем линейных алгебраических уравнений

Пусть требуется решить систему линейных алгебраических уравнений

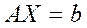, (1)

где 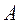-квадратная невырожденная матрица.

Перепишем матричное уравнение (1) в виде

,

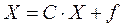где, например, матрица C = E – A (в этом случае ).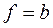

В результате может быть организован итерационный процесс, в ходе которого, начиная с некоторого вектора 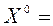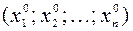^T , строится последовательность 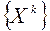в соответствии с рекуррентной формулой:

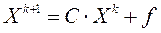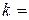, 0, 1, 2, ... .

Если при этом существует предел 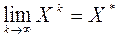, где 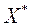решение системы (1), то итерационный процесс считают сходящимся.

В отличие от прямых методов решение системы с помощью итерационных методов можно получить лишь с некоторой погрешностью, которая обусловлена критерием остановки расчетов. При этом обычно используют норму вектора невязки или норму разности 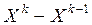, т.е., если требуется получить решение с точностью 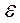>0, то расчеты выполняются до тех пор, пока не будет выполнено одно из условий:

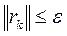или .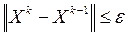

Итерационные методы, как правило, легко программируются, но иногда очень медленно сходятся или даже расходятся (если не выполнены условия сходимости). Для того, чтобы тот или иной итерационный процесс сходился, матрица 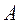должна удовлетворять определенным требованиям, а скорость сходимости зависит от вида матрицы . Для ускорения сходимости можно использовать итерационные методы с числовым параметром :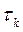

,

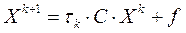где параметр 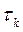может выбираться на каждом шаге либо быть константой.

Метод Якоби

Дана система линейных уравнений

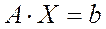, (1)

где, как и раньше, 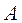– квадратная невырожденная матрица. Матрицу 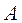всегда можно представить в ви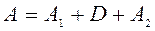де , где

; ; .

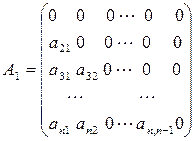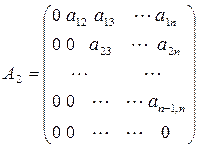Тогда матричное уравнение (1) можно переписать в виде:

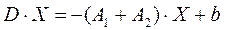. (1a)

Уравнение (1a) преобразуем в реккурентную формулу метода Якоби:

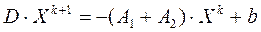, k = 0,1,2,…. (2)

Вычитая из обеих частей (2) 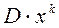получим представление (2) в виде:

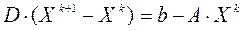, k = 0,1,2,…. (2a)

Обозначив 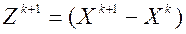и получим следующие расчетные формулы метода Якоби:

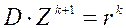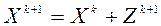; , k = 0,1,2,…. (3)

Вектор 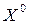можно взять любой, например, вектор 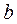или нулевой вектор.

Из (2) можно получить расчетные формулы для 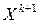в координатной форме:

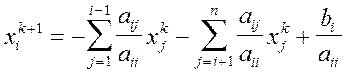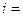; 1, ... n, 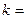0, 1, ... .(4)

В качестве критерия остановки расчетов обычно используют .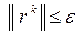

В матричном виде описание одного шага метода следующее:

1) вычисляем 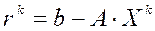, если 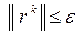, то вычисление закончены;

2) находим ;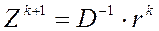

3) вычисляем .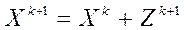

Итерационный процесс сходится, если

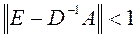(5).

Для симметричной положительно определенной матрицы 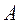для сходимости метода достаточно выполнения условия 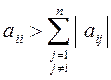, 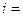1,..., n,

т.е. условия преобладания главной диагонали матрицы .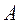

В случае, когда (5) не выполнено, необходимо преобразовать систему (1) таким образом, что бы условие сходимости было выполнено.

Задача

Решить систему уравнений: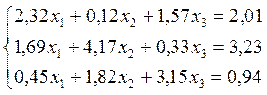

при помощи метода Якоби с точностью .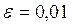

Решение.

; .

.

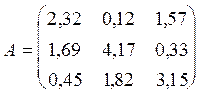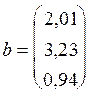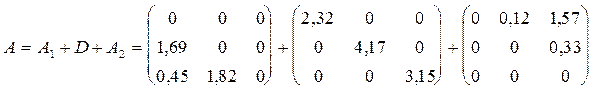Проверим условие сходимости: 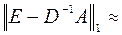0,756<1. Условие выполнено. Пусть 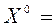(0; 0; 0)^T. Следующие расчеты приведены в таблице.

K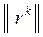
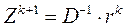
	3,919	(0,866; 0,775; 0,298)T	(0,866; 0,775; 0,298)T
	2,449	(–0,242; –0,375; –0,571)T	(0,624; 0,400; –0,273)T
	1,367	(0,406; 0,143; 0,251)T	(1,030; 0,543; –0,022)T
....	.....	.........	.........
	0,011	(–0,002; –0,001; –0,002)T	(0,892; 0,418; –0,072)T
	0,007

Так как 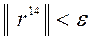, вычисления прекращаем.

Ответ: x₁ = 0,89; x₂ = 0,42; x₃ = -0,07.

Примечание. Если использовать модификацию метода Якоби с регулировкой шага: 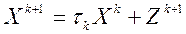, где 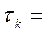0,8 (получено подбором), то этот же результат будет получен на 9-ой итерации.

Метод Зейделя

Дана система линейных уравнений

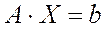,(1)

где 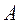-квадратная невырожденная матрица.

Представив A в виде суммы двух матриц 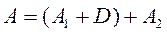, где 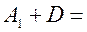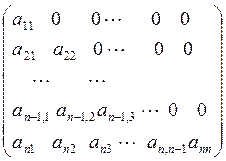; 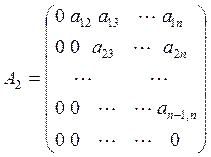, запишем (1) в виде:

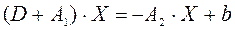(1a)

Уравнение (1a) преобразуем в реккурентную формулу метода Зейделя:

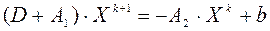, k = 0,1,2,… (2)

Вычитая из обеих частей (2) 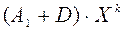, получим представление (2) в виде:

, k = 0,1,2,… (2a)

Обозначив 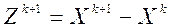, , 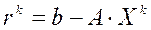получим расчетные формулы метода Зейделя в матричном виде:

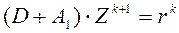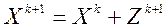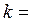; , 0, 1, ... (3).

Из (2) можно получить расчетные формулы для 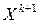в координатной форме:

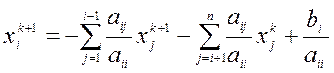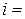, 1, ..., n, 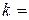0, 1, ... . (4)

Таким образом, метод Зейделя отличается от метода Якоби тем, что, найдя 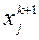, его сразу используют для вычисления 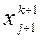(по начальным 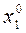, , 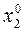..., 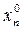находят 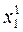, затем, используя 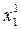, , ..., , 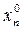находят 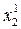и т.д.).

В качестве 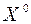можно взять любой, например, нулевой вектор. Критерий остановки расчетов: . Условием сходимости метода Зейделя является

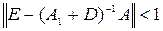(5).

Если A – симметричная положительно определенная матрица, то итерационный процесс Зейделя сходится всегда.

В матричном виде описание одного шага следующее:

1) вычисляем 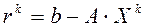, если 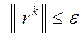то вычисления прекращаем;

2) находим ;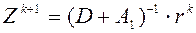

3) вычисляем .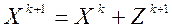

Здесь следует отметить, что при практической реализации метода Зейделя, как правило, матрицу 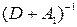не строят, а для построения очередного приближения пользуются рекуррентной формулой (4).

Задача

Решить систему из п.5.1 при помощи метода Зейделя с точностью = 0,01.

Решение.

; .

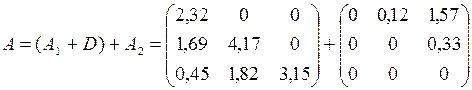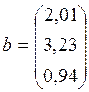Проверим условие сходимости: 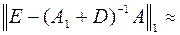0,888<1. Условие выполнено.

Пусть 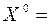(0; 0; 0)^T. Следующие расчеты приведены в таблице.

K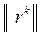
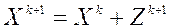
	3,919	(0,866; 0,423; –0,070)T	(0,866; 0,423; –0,070)T
	0,063	(0,025; –0,005; –0,001)T	(0,891; 0,418; –0,071)T
	0,002

Поскольку 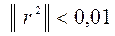, вычисления прекращаем.

Ответ: x₁ = 0,89; x₂ = 0,42; x₃ = -0,07.