Использование матриц вращения для решения систем
Матрицей вращения называется ортогональная матрица 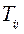 размерности
размерности 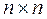 , полученная из единичной матрицы
, полученная из единичной матрицы 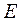 этой же размерности заменой 4–х элементов:
этой же размерности заменой 4–х элементов:
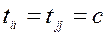 ;
; 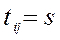 ;
; 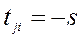 ; где
; где 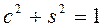
Матрица 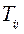 имеет вид:
имеет вид:
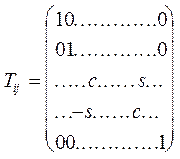
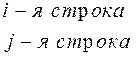
Пусть требуется решить систему линейных уравнений с невырожденной квадратной матрицей:
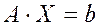 . (1) Если величины
. (1) Если величины 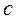 и
и 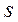 вычислить по формулам
вычислить по формулам
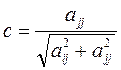 ;
; 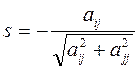 , (2)
, (2)
то, умножив матрицу А на 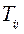 слева, получим
слева, получим 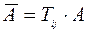 , где
, где 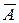 отличается от
отличается от 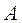 только двумя строками (
только двумя строками ( 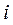 –ой и
–ой и 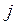 –ой), причем
–ой), причем 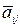 = 0. Например, левостороннее умножение системы (1) на матрицу
= 0. Например, левостороннее умножение системы (1) на матрицу 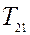 , приводит к эквивалентной системе
, приводит к эквивалентной системе
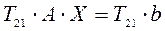 ,(*)
,(*)
при этом изменяются 1–я и 2–я строки матрицы системы и 1–ый и 2–ой элементы столбца правых членов системы, а элемент новой матрицы, находящийся на пересечении второй строки и первого столбца, становится равным нулю. Далее умножаем систему (*) слева на 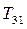
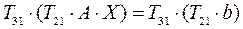 и т.д.
и т.д.
Для приведения исходной системы линейных уравнений к эквивалентной ей системе с верхней треугольной матрицей необходимо последовательно умножить (1) слева на цепочку ортогональных матриц
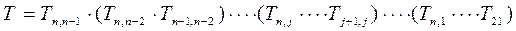 .
.
Таким образом, всего потребуется 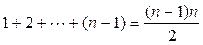 левосторонних умножений на матрицу вращения. Поскольку при каждом из таких умножений изменяются только 2 строки матрицы предыдущей системы и 2 элемента столбца
левосторонних умножений на матрицу вращения. Поскольку при каждом из таких умножений изменяются только 2 строки матрицы предыдущей системы и 2 элемента столбца 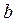 , то умножения
, то умножения
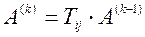 ,
, 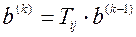 (4)
(4)
можно осуществлять по следующим формулам.
Для k = 0 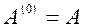 ;
; 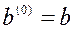 .
.
Далее для k =1,2....; j = 1, 2, ...n -1; i = j +1, j+2, ...,n.
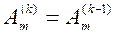 ;
; 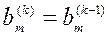 , если
, если 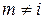 ,
, 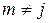
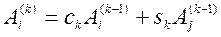 ;
; 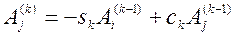 ; (5)
; (5)
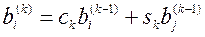 ;
; 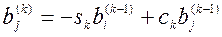 ;
;
где 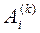 ,
, 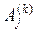 –
– 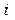 –я и
–я и 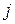 –я строки матрицы
–я строки матрицы 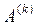 ;
; 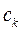 и
и 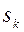 вычислены по формулам (2) с использованием элементов матрицы
вычислены по формулам (2) с использованием элементов матрицы 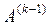 . Для удобства вычислений используют расширенную матрицу вида (A÷b), где (n+1)-ый столбец матрицы – это столбец свободных членов
. Для удобства вычислений используют расширенную матрицу вида (A÷b), где (n+1)-ый столбец матрицы – это столбец свободных членов 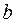 (см. п. 4.1.1).
(см. п. 4.1.1).
Задача
Решить систему с использованием матриц вращения:
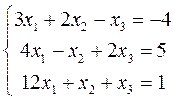 . Точность
. Точность 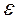 = 0,01.
= 0,01.
Решение. Прямой ход.
k = 0. Построим расширенную матрицу
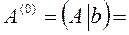
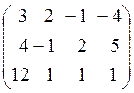 .
.
k = 1. Для обнуления элемента 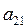 строим матрицу
строим матрицу 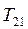 :
:
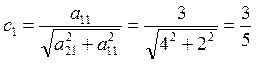 ;
; 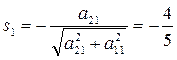 .
.
Находим строки матрицы 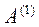 .
. 
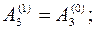
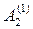 =
= 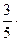 (4; –1; 2; 5) –
(4; –1; 2; 5) – 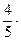 (3; 2; –1; -4) = (0; –2,2; 2; 6,2);
(3; 2; –1; -4) = (0; –2,2; 2; 6,2);
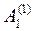 =
= 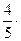 (4; –1; 2; 5) +
(4; –1; 2; 5) + 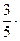 (3; 2; –1; -4) = (5; 0,4; 1; 1,6).
(3; 2; –1; -4) = (5; 0,4; 1; 1,6).
Результат: 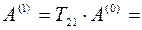
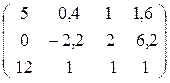 .
.
k = 2. Для обнуления элемента 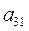 строим
строим 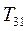 :
:
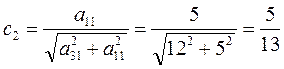 ;
; 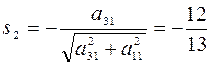 .
.
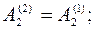
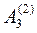 =
= 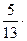 (12; 1; 1; 1) –
(12; 1; 1; 1) – 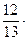 (5; 0,4; 1; 1,6)
(5; 0,4; 1; 1,6) 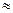 (0; 0,015; –0,538; -1,092);
(0; 0,015; –0,538; -1,092);
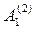 =
= 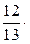 (12; 1; 1; 1) +
(12; 1; 1; 1) + 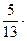 (5; 0,4; 1; 1,6)
(5; 0,4; 1; 1,6) 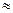 (13; 1,077; 1,308; 1,538).
(13; 1,077; 1,308; 1,538).
Результат 2-го шага:
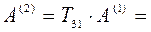
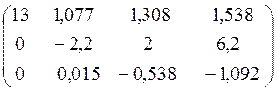 .
.
k = 3. Для обнуления элемента 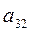 строим
строим 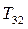 :
:
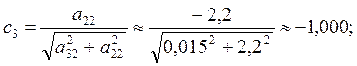
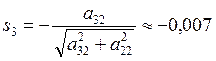 .
. 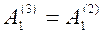 ;
;
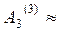 - (0; 0,015; –0,538; -1,092) – 0,007(0; –2,2; 2; 6,2)
- (0; 0,015; –0,538; -1,092) – 0,007(0; –2,2; 2; 6,2) 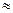
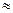 (0; 0; 0,524;1,049);
(0; 0; 0,524;1,049);
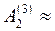 0,007(0; 0,015; –0,538;-1,092) – (0; –2,2; 2; 6,2)
0,007(0; 0,015; –0,538;-1,092) – (0; –2,2; 2; 6,2) 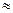
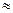 (0; 2,2; –2,004; -6,208).
(0; 2,2; –2,004; -6,208).
Результат 3-го шага:
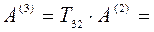
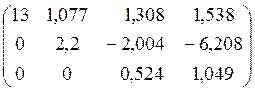 .
.
Обратный ход:
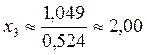 ;
; 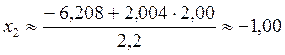 ;
;
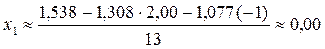 .
.
Ответ: 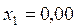 ;
; 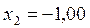 ;
; 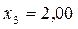 .
.
4.5.2 Использование матриц отражения для решения систем
Матрицей отражения 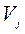 называется ортогональная матрица размерности
называется ортогональная матрица размерности 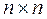 , полученная из единичной матрицы
, полученная из единичной матрицы 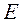 этой же размерности следующим образом:
этой же размерности следующим образом:
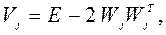
где 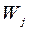 – единичный вектор (
– единичный вектор ( 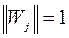 ),
), 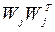 – матрица
– матрица 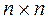 .
.
Если вектор 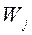 получен с использованием элементов
получен с использованием элементов 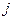 –го столбца матрицы А по формулам
–го столбца матрицы А по формулам
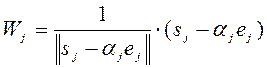 ; где
; где
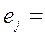 (0; 0; ..0; 1; 0; ...; 0)T, (единица на
(0; 0; ..0; 1; 0; ...; 0)T, (единица на 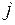 -м месте);
-м месте);
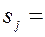 (0; 0; ...0;
(0; 0; ...0; 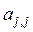 ;
; 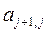 .....
..... 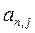 )T;
)T; 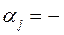
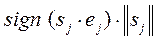 ,
,
то, умножив матрицу А на 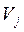 слева, получим матрицу
слева, получим матрицу 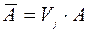 , в которой все поддиагональные элементы j-го столбца
, в которой все поддиагональные элементы j-го столбца 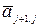 , ...,
, ..., 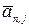 равны нулю.
равны нулю.
Дата добавления: 2021-07-22; просмотров: 509;











