Схема оптимального исключения

Данная схема отличается от классической тем, что на k-ом шаге получают нули не во всем столбце расширенной матрицы, а только над диагональным элементом 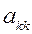, а перед этим обнуляют элементы k-ой строки левее .

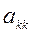Описание алгоритма.

1). Номер ведущей строки k = 1. Делим 1-ю строку на :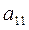

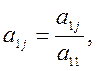j = 1, 2, ...,n + 1. и переходим к 5 пункту

2). Из k-ой строки вычитаем строки с номерами i = 1, 2, ... , k-1, умноженные на 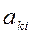с тем, чтобы получить нули левее :

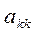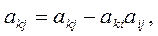j = 1, 2, ...,n + 1; i < k.

3). Делим k-ю строку на 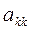, получая единицу на главной диагонали:

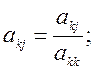j = k, k+1, ...,n + 1.

4). Из строк с номерами i =1, 2, ... , k-1 вычитаем k-ю строку, умноженную на 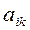с тем, чтобы получить нули над :

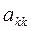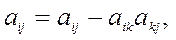j = k, k+1, ...,n + 1; i < k.

В результате выполнения k-го шага расширенная матрица примет вид:

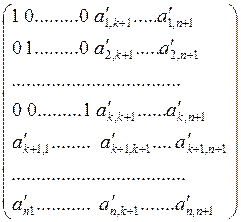
5). Увеличиваем номер шага k = k+1 и, если k 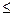n, переходим ко второму пункту.

Реализация схем Жордана требует примерно такого же количества арифметических операций, как и схемы Гаусса. Схема оптимального исключения позволяет экономить память ЭВМ за счет того, что рабочая часть расширенной матрицы на k-м шаге содержит только k строк, нет необходимости хранить всю матрицу, равно как и нулевые элементы в уже обработанной части матрицы. Необходимое для использования схем Жордана условие: 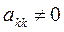. Если элементы главной диагонали матрицы 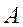в процессе работы метода оказываются равными или близкими к нулю, то можно использовать модификации метода с перестановкой строк или столбцов, аналогичные соответствующим модифиациям метода Гаусса.

Задача

Решить систему уравнений из п. 4.1.2:

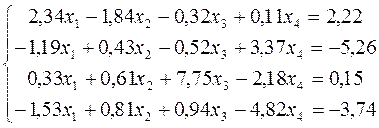
с использованием схем Жордана.

Решение. 1). Классическая схема Жордана.

№ шага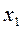
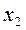
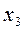
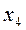
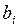
k=0	2,34	-1,84	-0,32	0,11	2,22
	-1,19	0,43	-0,52	3,37	-5,26
	0,33	0,61	7,75	-2,18	0,15
	-1,53	0,81	0,94	-4,82	-3,74
k=1		-0,786	-0,137	0,047	0,949
		-0,506	-0,683	3,426	-4,131
		0,869	7,795	-2,196	-0,163
		-0,393	0,731	-4,748	-2,288
k=2			0,925	-5,280	7,372
			1,350	-6,774	8,169
			6,621	3,695	-7,265
			1,261	-7,411	0,922
k=3				-5,796	8,387
				-7,528	9,650
				0,558	-1,097
				-8,115	2,307
k=4					6,739
					7,510
					-0,939
					-0,284

Ответ округляем с точностью до 0,01: x₁ = 6,74; x₂ = 7,51; x₃ = -0,94; x₄ = -0,28. Получили тот же результат, что и при помощи схемы Гаусса.

2). Схема оптимального исключения. Записываем в таблицу только рабочую часть расширенной матрицы, т.к. остальные строки не преобразовываются.

№ шага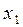
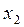
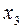
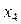
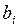
k=0	2,34	-1,84	-0,32	0,11	2,22
	-1,19	0,43	-0,52	3,37	-5,26
	0,33	0,61	7,75	-2,18	0,15
	-1,53	0,81	0,94	-4,82	-3,74
k=1		-0,786	-0,137	0,047	0,949
k=2			0,925	-5,280	7,372
			1,350	-6,774	8,169
k=3				-5,796	8,387
				-7,528	9,650
				0,558	-1,097
k=4					6,739
					7,510
					-0,939
					-0,284

Ответ: x₁ = 6,74; x₂ = 7,51; x₃ = -0,94; x₄ = -0,28.

Метод Холецкого.

Метод Холецкого также относится к прямым методам решения системы линейных уравнений с невырожденной квадратной матрицей:

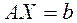(1)

Если представить матрицу 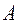в виде произведения 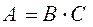, где , ,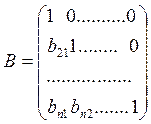

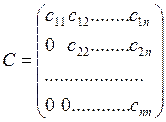то система (1) примет вид:

.

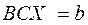Обозначив 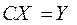, получаем 2 системы с треугольными матрицами:

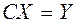(2)

и

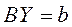, (3)

которые легко решаются. Решая (3), а затем (2), получаем решение системы (1)- вектор Х.

Самый трудоемкий этап метода Холецкого - вычисление элементов матриц B и C (прямой ход). Элементы этих матриц 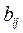и 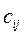находят “ёлочкой”, т.е. по схеме: строка матрицы C - столбец матрицы B. Прямой ход завершается вычислением значений 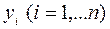. Обратный ход - вычисление .

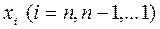Описание алгоритма и расчётные формулы.

Прямой ход.

1) Для k=1 вычисляем элементы 1-ой строки матрицы С и элементы 1-го столбца матрицы В:

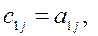j = 1...n; 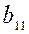= 1; 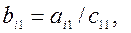i = 1..n. (4)

2) Для 1<k<n находим элементы k-ой строки матрицы C и k-го столбца матрицы В по формулам:

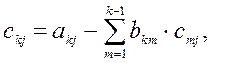j = k, k+1,...n. (5) 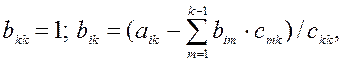i = k+1, k+2,...n. (6)

3) Для k = n находим 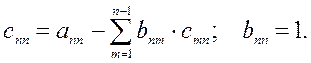(7)

Для контроля проверяют выполнение условия BC = A.

4) Находим решение системы (3) по формулам: 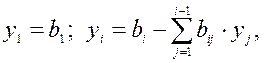i = 2, 3,...n.

Здесь 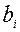- свободные члены системы (1), 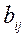- элементы матрицы В.

5) Обратный ход. Находим решение системы (2) по формулам: 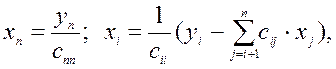i = n-1, n-2,....2, 1.

Здесь 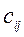-элементы матрицы С.

Задача

Решить систему уравнений из п.4.2.2, используя метод Холецкого:

Решение. Прямой ход.

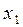
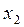
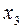
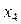
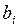
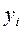
	2,34	-1,84	-0,32	0,11	2,22	2,22
A	-1,19	0,43	-0,52	3,37	-5,26	-4,131
	0,33	0,61	7,75	-2,18	0,15	-7,265
	-1,53	0,81	0,94	-4,82	-3,74	2,307
	Разложение матрицы А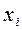
	2,34	-1,84	-0,32	0,11	6,739
		-0,506	-0,683	3,426	7,510
B\C	-0,509		6,621	3,695	-0,939
	0,141	-1,719		-8,115	-0,284
	-0,654	0,777	0,191

Подробные формулы.

1)

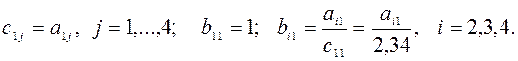
2) 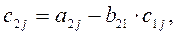j = 2, 3, 4; 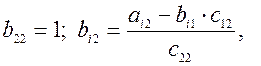i 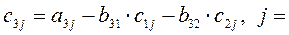= 3,4.

3,4;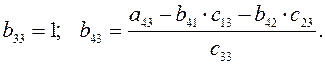

3)

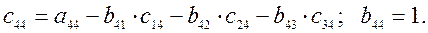
4)

.

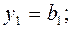
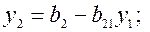
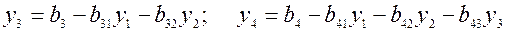Обратный ход.

5)

.

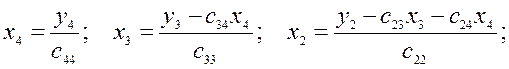
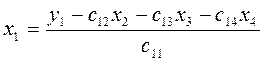Ответ: x₁ = 6,74; x₂ = 7,51; x₃ = -0,94; x₄ = -0,28.