Метод квадратных корней

Этот метод используется для решения системы

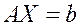(1)

в случае симметричной невырожденной матрицы 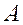( 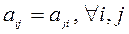). Идея метода - представить матрицу 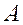в виде произведения 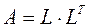, где 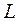- нижняя треугольная матрица:

.

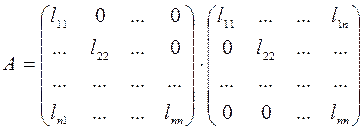По сути, метод квадратных корней является частным случаем метода Холецкого ( 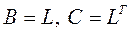) и поэтому схема решения та же: из (1) получаем LL^TX = b, обозначаем L^TX = Y и решаем сначала LY = b, затем L^TX = Y. За счет симметрии матрицы 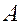формулы упрощаются, и в итоге число арифметических операций получается примерно вдвое меньше, чем в схемах исключения (порядка 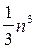). Поскольку можно хранить лишь 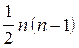элементов матрицы 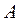, получаем значительную экономию памяти ЭВМ.

Описание алгоритма и расчетные формулы. Прямой ход

1) Находим 1-ый столбец матрицы L:

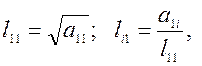i = 2, 3,...n. (2)

2) Находим элементы k-го столбца матрицы L для k = 2, 3,...,n.

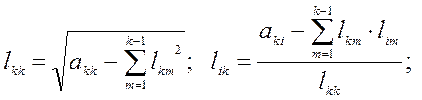i = k+1, k+2,...n. (3)

3) Вычисляем элементы столбца Y:

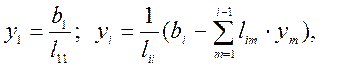i = 2, 3,...n. (4)

4) Находим решение системы (1):

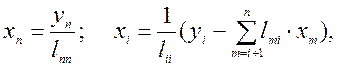i = n-1, n-2,...2, 1. (5)

Задача

Решить систему уравнений, используя метод квадратных корней.

.

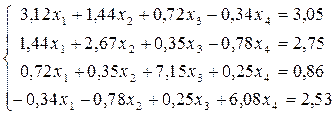Решение. Прямой ход.

i	L\A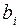
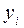
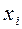
	1,766	3,12	1,44	0,72	-0,34	3,05	1,727	0,651
	0,815	1,416	2,67	0,35	-0,78	2,75	0,948	0,843
	0,408	0,012	2,643	7,15	0,25	0,86	0,055	-0,006
	-0,192	-0,440	0,126	2,415	6,08	2,53	1,355	0,561

Подробные формулы.

1)

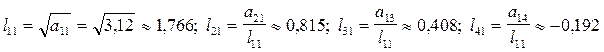
2)

.

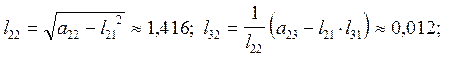
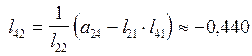3) .

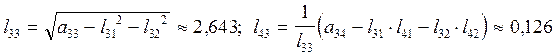4) .

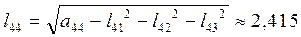5)

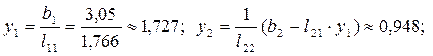
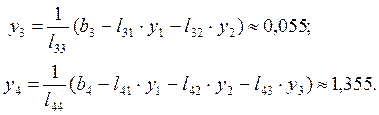
Обратный ход.

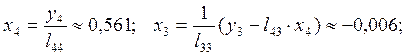
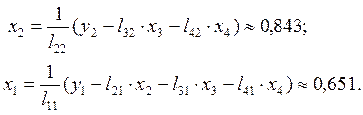
Вектор невязок: 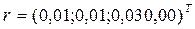. Норма вектора невязок: 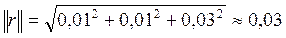. Ответ: x₁ = 0,65; x₂ = 0,84; x₃ = -0,01; x₄ = 0,56.

Метод прогонки

Пусть дана система линейных уравнений с невырожденной трехдиагональной матрицей:

.

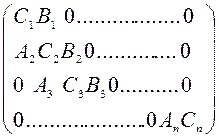Такую систему можно записать в виде: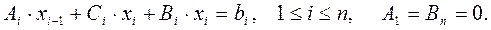

Для ее решения может быть использован метод прогонки, относящийся к методам исключения, но использующий особенности трехдиагональной матрицы.

Метод прогонки состоит из прямого и обратного хода.

Прямой ход заключается в определении коэффициентов, связывающих 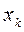и :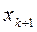

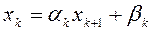, k = 1,2,...n-1.

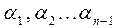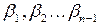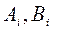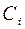В результате прямого хода находят коэффициенты прогонки и через коэффициенты и . Обратный ход - вычисление 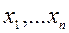, начиная с последнего.

Описание алгоритма и расчётные формулы.

Прямой ход метода прогонки.

Находим 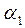и 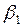: 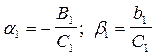. Вычисляем 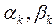для k = 2, 3, ...n-1.:

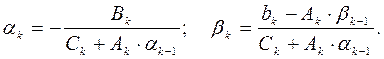
Обратный ход метода прогонки.

Находим .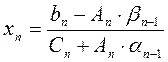

Вычисляем 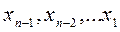по формулам:

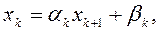k = n-1, n-2, ..1.

Поскольку при решении задачи на ЭВМ нужно хранить в памяти только ненулевые элементы 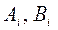, , 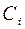то такая структура матрицы позволяет экономить память. Сокращается также время расчётов, т.к. операции с нулевыми элементами не производятся: вычисления методом прогонки осуществляются примерно в 9n арифметических операций. Таким образом, этот метод намного экономнее других методов исключения.

Если в матрице А выполнено условие преобладания главной диагонали 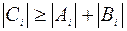а также некоторые дополнительные условия, то метод прогонки устойчив к ошибкам округления..

Задача

Решить методом прогонки следующую систему уравнений:

.

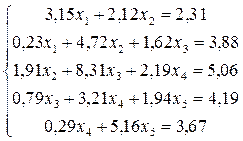Решение.

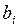
Коэффициенты при неизвестных		Прогонка
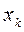
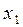
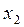
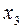
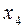
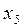
					k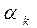
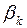
3,15	2,12				2,31		-0,673	0,733	0,238
0,23	4,72	1,62			3,88		-0,355	0,813	0,737
	1,91	8,31	2,19		5,06		-0,287	0,460	0,215
		0,79	3,21	1,94	4,19		-0,650	1,283	0,851
			0,29	5,16	3,67				0,663

Подробные вычисления.

Прямой ход метода прогонки.

;

;

;

.

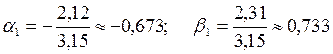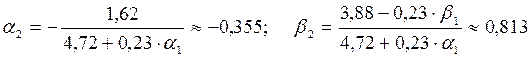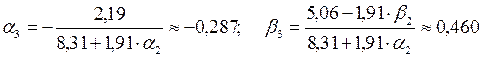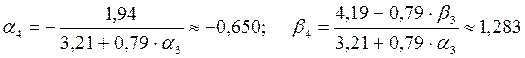Обратный ход метода прогонки.

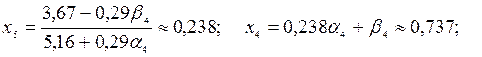
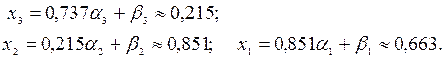
Вектор невязок: .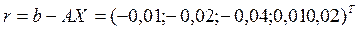

Норма вектора невязок: .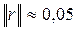

Ответ: x₁ = 0,66; x₂ = 0,85; x₃ = 0,22; x₄ = 0,74; x₅ = 0,24.

4.5 Прямые методы решения систем уравнений, основанные на ортогональных преобразованиях

Дана система линейных уравнений:

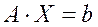. (1)

Ортогональные преобразования системы (1) осуществляются, в частности, посредством левостороннего умножения матрицы системы А и вектора правых частей b матричного уравнения (1) на ортогональную матрицу 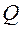: 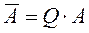; 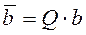. В результате такого умножения система (1) может быть заменена на эквивалентную ей систему: 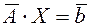. С помощью определенным образом организованной последовательности таких умножений можно преобразовать исходную систему линейных уравнений к эквивалентной ей системе с верхней треугольной матрицей (прямой ход). Обратный ход осуществляется в этом случае так же, как в схемах Гаусса (см. п.4.1).