Малые свободные колебания системы с одной степенью свободы.
Произведем разложение функций A(q) и П(q) в ряды Маклорена вблизи точки q= 0; получим:
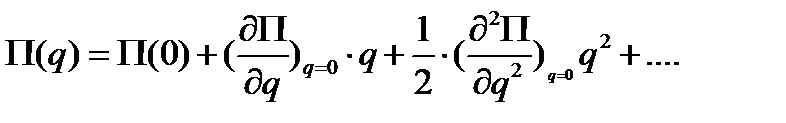 (5.2)
(5.2)
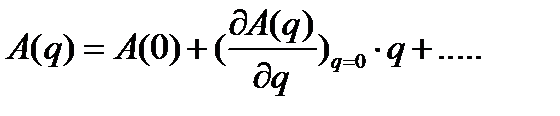
Отбрасывая несущественную постоянную в выражении потенциальной энергии, можем положить П(0) = 0; кроме того, как ранее уже было показано, в положении равновесия системы равна нулю первая производная от потенциальной энергии. Вторая производная от потенциальной энергии в положении устойчивого равновесия удовлетворяет условию 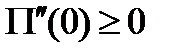 , где знак равенства относится к тому случаю, когда о наличии минимума потенциальной энергии приходится заключать по старшим производным. Примем
, где знак равенства относится к тому случаю, когда о наличии минимума потенциальной энергии приходится заключать по старшим производным. Примем
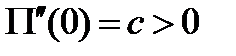
Коэффициент с называют коэффициентом жёсткости или коэффициентом квазиупругости. Правильную, по крайней мере качественно, картину движения при любом t можно получить, сохраняя в разложениях потенциальной и кинетической энергии лишь члены наинизшего порядка относительно q и 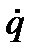 . Из равенств (3.52) получим:
. Из равенств (3.52) получим: 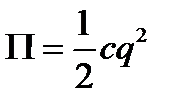 (5.3)
(5.3)
Подставляя в выражение для кинетической энергии (4.35) разложение A(q) согласно (5.2), найдем:
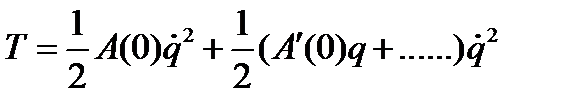
или в принятом приближении:
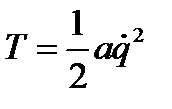 (5.4)
(5.4)
где по условию положительности кинетической энергии всегда будет: 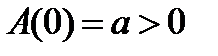 . Коэффициент а носит название коэффициент инерции.
. Коэффициент а носит название коэффициент инерции.
Имея выражения (5.3) и (5.4) для потенциальной и кинетической энергий, составим уравнения движения системы в форме Лагранжа, в нашем случае уравнение движения будет: 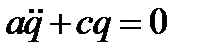 или
или 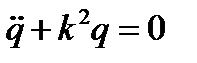 , где
, где 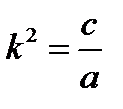 . Сравнивая его с известным из школьного курса физики уравнением прямолинейных свободных колебаний точки под действием упругой восстанавливающей силы, видим, что коэффициент а при обобщенном ускорении
. Сравнивая его с известным из школьного курса физики уравнением прямолинейных свободных колебаний точки под действием упругой восстанавливающей силы, видим, что коэффициент а при обобщенном ускорении 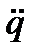 играет ту же роль, что и масса m точки, т. е. характеризует инерционность системы, а коэффициент с аналогичен коэффициенту упругости.
играет ту же роль, что и масса m точки, т. е. характеризует инерционность системы, а коэффициент с аналогичен коэффициенту упругости.
Общий интеграл этого уравнения имеет вид:
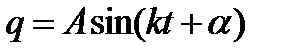
где амплитуда А и начальная фаза α определяются по начальным условиям. Пусть при 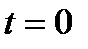
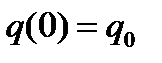 и
и 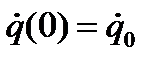 , тогда
, тогда
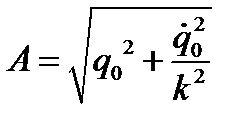 и
и 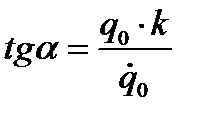 (5.5)
(5.5)
Это - свободные или собственные колебания системы. Частота, или период, свободных колебаний системы не зависит ни от начальных условий движения (изохронизм малых колебаний), ни от природы обобщенной координаты; они представляют основные константы системы, определяемые структурой выражений кинетической и потенциальной энергий, т. е. инерционными свойствами материальной системы и характером консервативного силового поля, в котором происходит колебательное движение системы. Из формул (5.3), (5.4) и (5.5) видно, что амплитуда колебаний А пропорциональна корню квадратному из полной энергии Е=Т+П системы. Движение представляет гармоническое колебание частоты k и периода 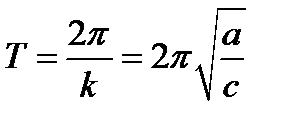 (в дальнейшем для периода сохраняется общепринятое обозначение Т, хотя этот символ уже использован для обозначения кинетической энергии).
(в дальнейшем для периода сохраняется общепринятое обозначение Т, хотя этот символ уже использован для обозначения кинетической энергии).
Качественное изучение общей картины движения системы облегчается введением в рассмотрение так называемой фазовой плоскости (q, 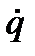 ), в которой строятся кривые — фазовые траектории, выражающие графически зависимость между обобщенной координатой q и обобщенной скоростью
), в которой строятся кривые — фазовые траектории, выражающие графически зависимость между обобщенной координатой q и обобщенной скоростью 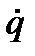 системы для всего многообразия интегральных кривых. Так, в только что рассмотренном случае свободных колебаний системы вокруг положения ее устойчивого равновесия фазовые траектории можно получить путем исключения времени t из уравнений:
системы для всего многообразия интегральных кривых. Так, в только что рассмотренном случае свободных колебаний системы вокруг положения ее устойчивого равновесия фазовые траектории можно получить путем исключения времени t из уравнений:
q = A sin (kt+ a), 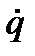 = k A cos (kt + a), чтo приведет к семейству кривых
= k A cos (kt + a), чтo приведет к семейству кривых
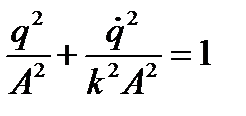
К тому же результату, очевидно, придем, написав уравнение семейства уровней полной механической энергии Е системы
|
| Рис 67 |
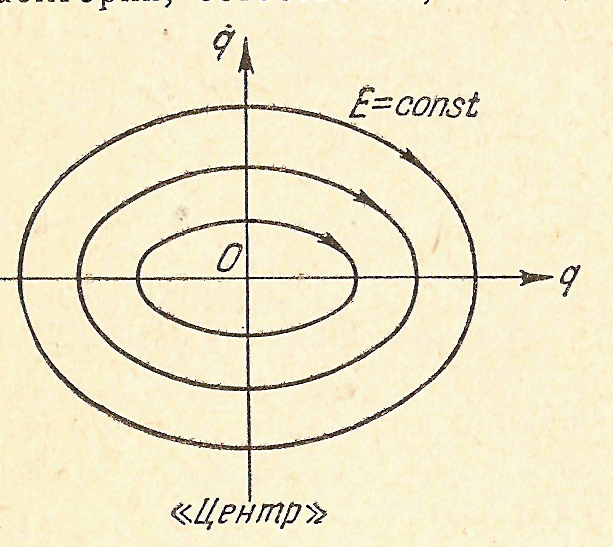
Е = Т+ П = 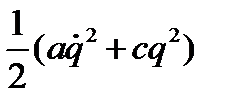 . В рассматриваемом случае консервативной системы фазовые траектории, естественно, совпадают с кривыми уровней энергии. Фазовыми траекториями служат подобные, между собою эллипсы, отличающиеся друг от друга только масштабом, зависящим от начальных условий движений или, точнее, от полной энергии системы (Рис 67). Для всех эллипсов отношение длин полуосей одно и то же, — оно равно частоте k собственных колебаний системы. Каждому движению системы при заданных начальных условиях соответствует движение изображающей точки в фазовой плоскости по фазовой траектории — эллипсу — в указанном на рисунке направлении.
. В рассматриваемом случае консервативной системы фазовые траектории, естественно, совпадают с кривыми уровней энергии. Фазовыми траекториями служат подобные, между собою эллипсы, отличающиеся друг от друга только масштабом, зависящим от начальных условий движений или, точнее, от полной энергии системы (Рис 67). Для всех эллипсов отношение длин полуосей одно и то же, — оно равно частоте k собственных колебаний системы. Каждому движению системы при заданных начальных условиях соответствует движение изображающей точки в фазовой плоскости по фазовой траектории — эллипсу — в указанном на рисунке направлении.
Рассмотрим общий интеграл уравнения 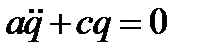 при условии с<0, соответствующем неустойчивости равновесия системы в положении q(0)= 0. Вводя в этом случае обозначение
при условии с<0, соответствующем неустойчивости равновесия системы в положении q(0)= 0. Вводя в этом случае обозначение 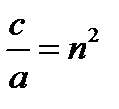 получим
получим
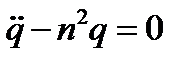
Общий интеграл этого уравнения выражается через показательные или гиперболические функции:
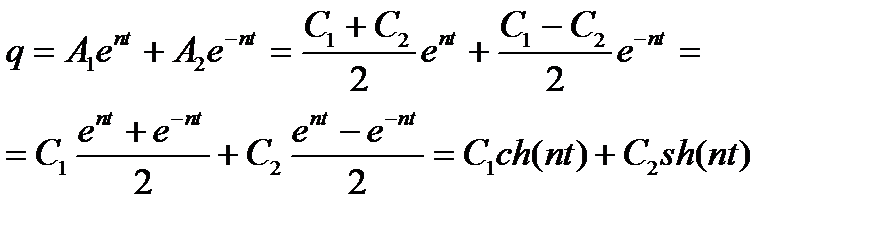
Как видно из полученного решения, в отличие от движения системы вблизи положения устойчивого равновесия, обобщенная координата q и обобщенная скорость  с ростом времени t могут приобретать сколь угодно большие значения. Найдем уравнение семейства фазовых траекторий, которое и в этом случае будет совпадать с уравнением семейства уровней полной механической энергии
с ростом времени t могут приобретать сколь угодно большие значения. Найдем уравнение семейства фазовых траекторий, которое и в этом случае будет совпадать с уравнением семейства уровней полной механической энергии
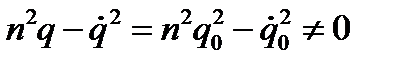 .
.
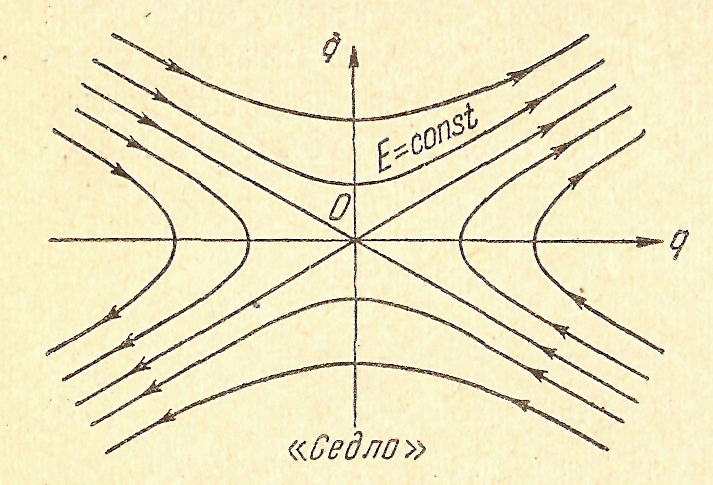
|
| Рис 68 |
Полученное уравнение представляет семейство подобных гипербол. Все гиперболы имеют одни и те же асимптоты, уравнения которых (рис 68)
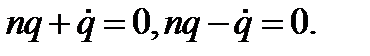
| М |
| О |
| А |
| В |
| m |
| Рис 69 |
| φ |
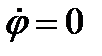 . ОА=ОВ=l,
. ОА=ОВ=l,  *).
*).
Сосчитаем потенциальную энергию по известной формуле для сил тяжести 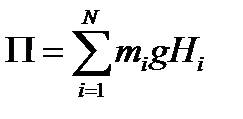
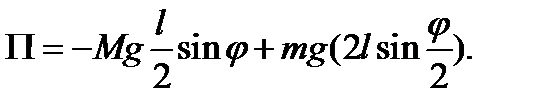
Равенство нулю первой производной от потенциальной энергии определит положения равновесия
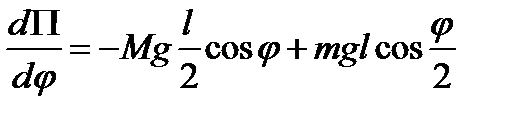
С учётом условия *) получаем тригонометрическое уравнение
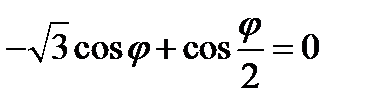
Перепишем полученное уравнение в другом виде
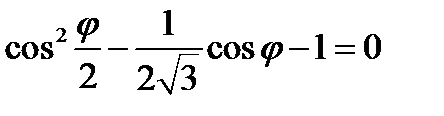 .
.
Решениями этого уравнения будут:
1. 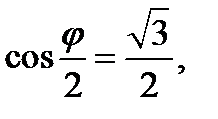 и
и 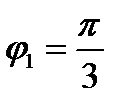 ;
;
2. 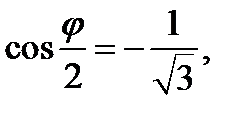 и
и 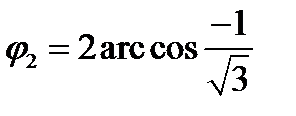 , т.е
, т.е 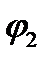 находится в третьей четверти. Устойчивость равновесия для полученных значений φ проверим по знаку второй производной от потенциальной энергии, с учетом формулы *) имеем
находится в третьей четверти. Устойчивость равновесия для полученных значений φ проверим по знаку второй производной от потенциальной энергии, с учетом формулы *) имеем
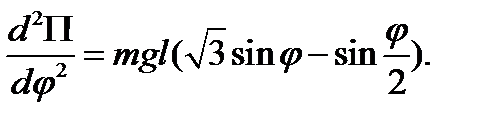
Для 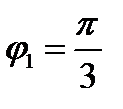 получаем
получаем 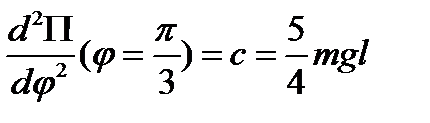 >0.
>0.
Для второго значения угла 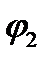 значение второй производной отрицательно, т.е. второе положение равновесия неустойчиво. Потенциальная энергия вблизи устойчивого положения равновесия будет иметь вид
значение второй производной отрицательно, т.е. второе положение равновесия неустойчиво. Потенциальная энергия вблизи устойчивого положения равновесия будет иметь вид
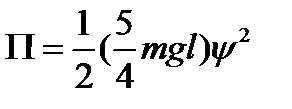 .
.
Сосчитаем кинетическую энергию системы
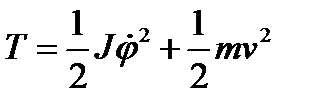 ,
,
здесь 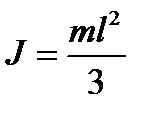 ,
, 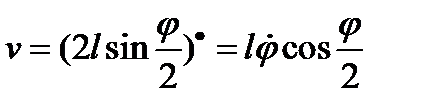 . Подставляя полученные соотношения в формулу для кинетической энергии, имеем
. Подставляя полученные соотношения в формулу для кинетической энергии, имеем
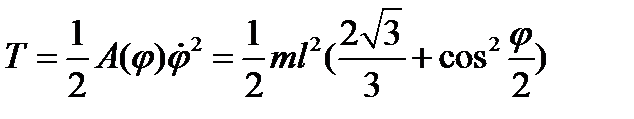 .
.
В положении устойчивого равновесия 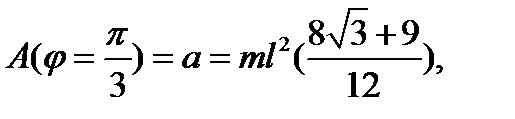
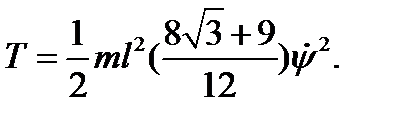
Дифференциальное уравнение малых колебаний запишется в виде
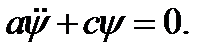
Здесь ψ – отклонение стержня от положения равновесия, т.е. 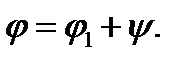 Частота колебаний
Частота колебаний 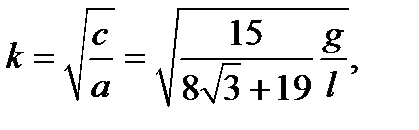 а решение дифференциального уравнения будет
а решение дифференциального уравнения будет
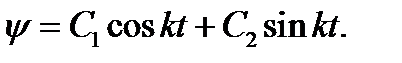
Для определения констант интегрирования воспользуемся начальными условиями 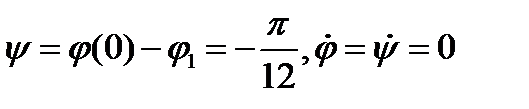 , тогда
, тогда 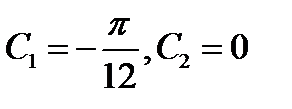 и получаем
и получаем
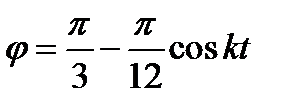
Дата добавления: 2019-12-09; просмотров: 688;











