Свободные колебания системы с учётом линейно-вязкого сопротивления.

В случае одночленной степенной зависимости сил сопротивления от скорости диссипативная функция

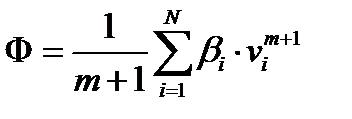
будет однородной функцией (m+1) степени от обобщенных скоро­стей. Отметим, что m = 0 соот­ветствует кулонову (сухому) трению, m=1—силам вязкого трения, пропорциональным первой степени скорости (случай Релея), m = 2 — силам квадратичного сопротивления. В случае малых колебаний системы, в принятом в предыдущем параграфе приближении, следует принять m=1. Тогда имеем

. (5.6)

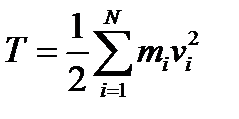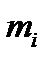Сравнивая (5.6) с формулой для кинетической энергии , заметим, что они отличаются лишь коэффициентами и , следовательно, для малых колебаний системы с одной степенью свободы получаем (по аналогии с (5.3), заменяя А(0) соответствующим коэффициентом В(0))

В принятом приближении диссипативная функция имеет вид

(5.7)

(здесь b=В(0)). Уравнение Лагранжа 2-го рода имеет вид

.

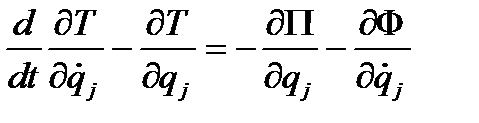Подставляя в него ранее полученные выражения для потенциальной и кинетической энергий, а также для диссипативной функции, получаем дифференциальное уравнение колебаний

,

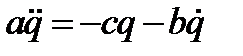которое в обычном виде записывается так

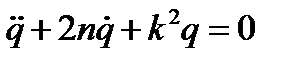, . (5.8)

Это линейное, однородное дифференциальное уравнение с постоянными коэффициентами, для решения которого необходимо получить характеристическое уравнение 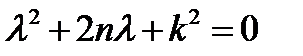. Корнями уравнения будут служить величины

Естественно рассмотреть отдельно следующие три случая дви­жения.

1. Затухающее колебательное движение (n<k). Если n<k, то корни характеристического уравнения пред­ставятся так:

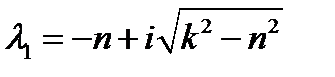и

и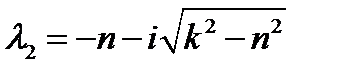, следовательно, общий интеграл уравнения (5.8) будет:

(5.9)

Составим первую производную по времени

(5.10)

Используем для определения постоянных интегрирования началь­ные условия: 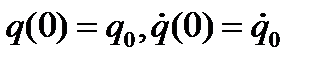при t=0. Подставляя эти значения координаты и скорости в (5.9) и (5.10), найдем:

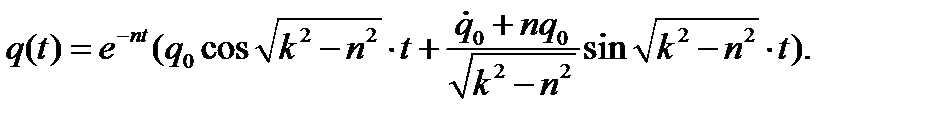(5.11)

или 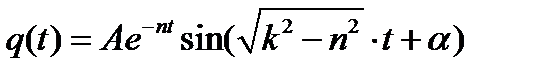, где для краткости положено

Из уравнения движения следует, что 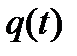перио­дически меняет знак, так что движение точки имеет колебатель­ный характер. Период колебания равен

где 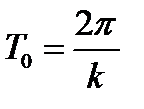представляет период свободных колебаний точки при отсутствии сил сопротивления. График затухающих колебаний

Рис 70

представлен на рисунке , на рис.70-

τ есть период колебаний. Пунктирная линия, огибающая график

.

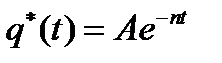Абсолютные величины максимальных отклонений образуют, геометрическую прогрессию со знаменателем 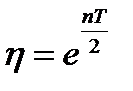. Действительно

Натуральный логарифм отношения двух последовательных ампли­туд носит наименование логарифмического декремента; он равен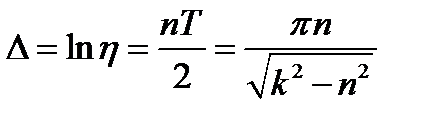

2. Апериодическое движение (n>k). При достаточно большом сопротивлении, когда , общий интеграл урав­нения (5.8) будет:

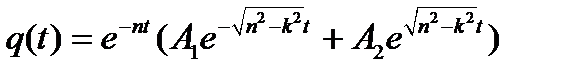
Движение не будет носить колебательного характера (оно назы­вается поэтому апериодическим). Полученному решению можно придать другой вид, если воспользоваться гиперболическими функциями .

Пусть

.

Тогда

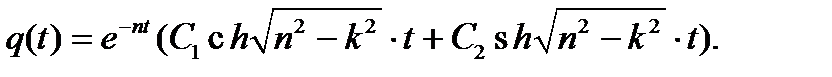
Составим первую производную по времени

и используем для определения постоянных интегрирования началь­ныеусловия: 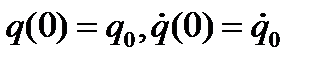при t=0. Подставляя эти значения координаты и скорости найдем

(5.12)

Вследствие бы­строго убывания показательной функции величина 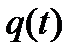будет весьма мала уже при небольших t, и систему можно практически считать вернувшейся в положение равновесия. Характер движения зависит от начальных условий. Графики движения системы представлены на рисунке 71. В случае а) 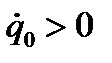, в случае б) и в) 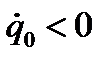. Случаи а) и б) соответствуют апериодическому движению пер­вого рода, случай в) — апериодическому движению второго рода.

3.Предельное апериодическое движение ( ).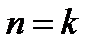

Общий интеграл уравнения (5.8) в данном случае будет иметь вид

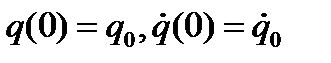
Начальные условия: при t=0. Получим

Рис 71

5.13)

График изменения такой же, как и для апериодического движения ( ) .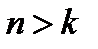

Рассмотрим пример, разобранный в предыдущем параграфе, но добавим силу сопротивления 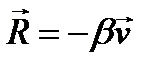, действующую на груз m. Функцию Рэлея запишем в виде или, подставляя значение для скорости 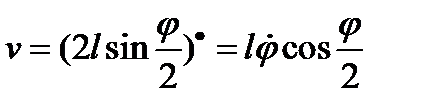, получим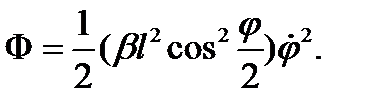

В положении равновесия

и дифференциальное уравнение будет иметь вид

или

Здесь .

Если , т.е. 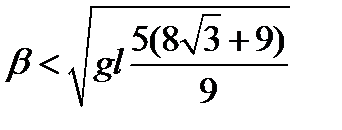, имеем затухающие колебания и решение записывается в форме (5.11), если , то апериодическое движение (5.12),(5.13).

Глава 17.