Работа силы. Мощность.

Для характеристики действия силы на материальную точку на

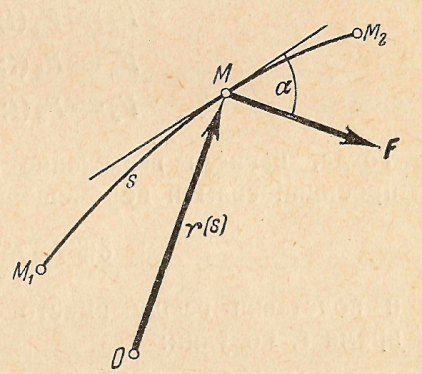
Рис 61

протяжении некоторого пути вводится мера этого действия, назы­ваемая работой силы. Сначала введем в рассмотрение понятие элементарной работы (рис 61). Будем определять положение точки М на кривой 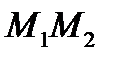дугой s, от­считываемой от точки 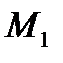. Вектор-радиус 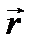точки М будет вектор-функцией 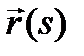от s. Работа силы 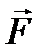на этом элементарном перемещении, или элемен­тарная работа 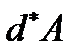определится выражением

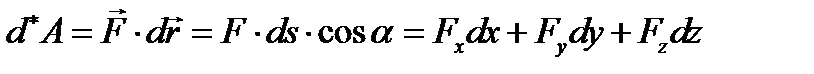
Если сила перпендикулярна к перемещению, то cosα = 0 и работа равна нулю; если сила направлена по перемещению cosα = l и работа равна произведению величины силы на величину перемещения, и, наконец, если сила направлена против движения, то cosα = - 1 и произведе­ние уже берется со знаком минус. Таким образом, в определении работы учитывается зависимость эффекта действия силы от направ­ления ее по отношению к перемещению. Измеряется работа в килограммометрах (кгм) в технической системе единиц, в эргах (дина см) или джоулях ( 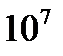эргов) - в физи­ческой системе. В общем же случае выражение 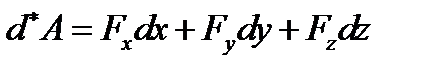не представляет полного дифференциала и символ 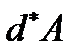следует по­нимать только как символ бесконечно малой величины, а отнюдь не дифференциала. В дальнейшем будет выяснено наличие частных классов сил, элементарная работа которых является полным дифференциалом некоторой функции от координат точки. Работа силы на конечном перемещении 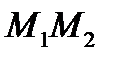определиться интегралом

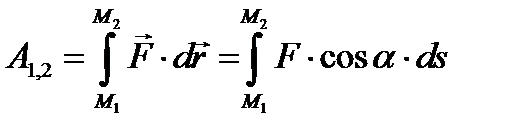
Интегрирование в полученном выражении производится по величинам, отнесенным к бесконечно малым дугам кривой 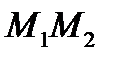. Поэтому этот интеграл называется криволинейным интегралом, взятым вдоль дуги кривой 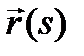от точки 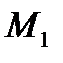до точки 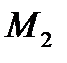. Такие интегралы (они называются криволинейными) часто встречаются в различных вопросах механики, гидроди­намики и электродинамики.

Рассмотрим несколько примеров, когда вычисление работы может быть сведено к вычислению простого определенного интеграла:

1. если движение происходит по прямолинейной оси, например по оси Ох, и сила являлась функцией одного только х, то элемен­тарная работа действительно представляет дифференциал .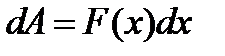

2. Предположим, что движение точки задано уравнениями 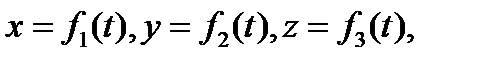и, кроме того, задан закон изменения силы в зависимости от изме­нения времени, координат и скорости. Тогда, написав выражение элементарной работы через проекции силы и перемещения на оси и подставив их выражения через время t, получим 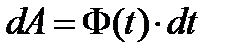,где Ф (t) - известная функция времени. Чтобы найти работу на пути 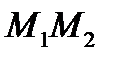, надо взять интеграл

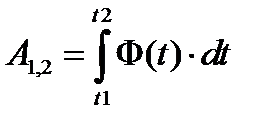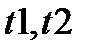, где - моменты, соответствующие прохождению движущейся точкой положени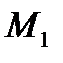й и 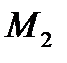. Задача свелась к вычислению опреде­ленного интеграла по аргументу t.

3. Область пространства, в каждой точке которого одно­значно определена некоторая функция, будем называть полем; в зависимости от того, будет эта функция скалярной, векторной или тензорной величиной, поле будет скалярным, векторным или тензорным. Так, скалярным полем будет тем­пературное поле, когда вокруг источника тепла (нагретого тела) в каждой точке окружающей это тело среды будет свое значение температуры. Для движущейся сплошной среды (жидкость, газ) поле скоростей точек этой среды явля­ется примером векторного поля. Примером тензорного поля может служить малая деформация среды — в каждой точке среды относительные удлинения и углы сдвига образуют не­который тензор, называемый тензором малых деформаций. Силовым полем называется область пространства, в каж­дой точке которой определен вектор силы 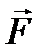, действующий на помещаемое в эту точку материальное тело. Силовое поле называется потенциальным, если сила пред­ставляет собой градиент скалярной функции. Рассмотрим свойства потенциальных силовых полей. По определению

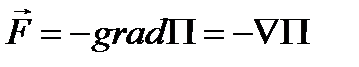, (3.91)

где оператор «набла» в декартовой системе координат равен

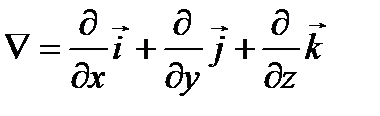
Здесь П = П(x, у, z) - потенциальная энергия (или по­тенциал) силового поля. Тогда

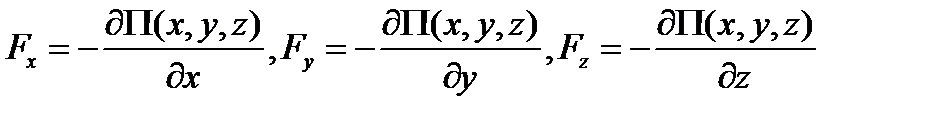
а это, в свою очередь, означает, что дифференциальная форма (элементарная работа)

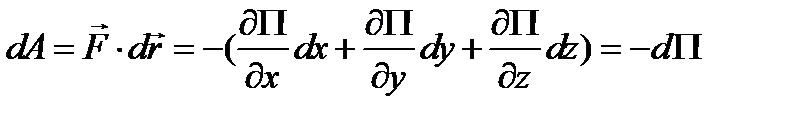(3.92)

в рассматриваемом случае будет полным дифференциалом. Итак, элементарная работа потенциальной силы является полным дифференциалом. Интегрируя соотношение (3.92) на конечном участке дви­жения точки (от 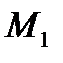до 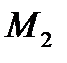, получим выраже­ние для работы на конечном участке пути

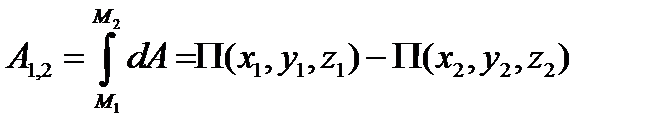
Правая часть полученного выражения зависит только от положе­ния (координат) начальной и конечной точек и, следователь­но, работа в потенциальном силовом поле не зависит от вида пути. Рассмотрим поверхность равного потенциала П (х, у, z) =const. Сила 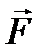направлена по нормали к поверхности равного потен­циала; знак «минус» в формуле (3.91) указывает, что потен­циальная сила направлена в сторону убывания потенциаль­ной энергии. Надо отметить, что потенциальная энергия была введена дифференциальным путём и поэтому определена с точностью до аддитивной постоянной; эта постоянная будет зафиксирована, если условиться об отсчёте потенциальной энергии от некоторого начального уровня. Желая охарактеризовать работу с точки зрения времени, в тече­ние которого она производится, вводят понятие мощности, как отно­шения произведенной работы к протекшему времени или как работу, отнесенную к единице времени. Обозначая мощность через N, можем написать:

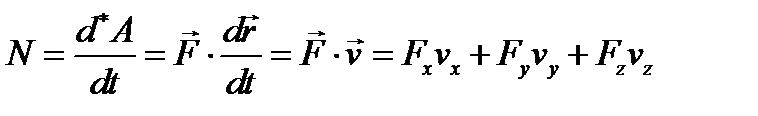
Мощность равна скалярному произведению векторов силы и скорости. За единицу мощности можно принять любую единицу работы, отнесенную к единице времени, т. е. эрг/сек, джоуль/сек, кГм/сек; обычно за единицу мощности принимают следующие единицы:

1 ватт= 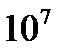эрг/сек = 1 джоуль/сек = 0,102 кГ м/сек,

1 киловатт =103 ватт= 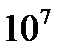эрг/сек= 102 кГ м/сек,

1 кГ м/сек =9,807 ватт,

1 л. с. (HP) = 75 кГ м/сек = 0,736 киловатт.

Иногда принято работу измерять в единицах мощности, умно­женных на единицу времени, т.е. в ватт • сек, в киловатт-часах и т.п.