Кинетическая энергия твердого тела.
В случае поступательного движениятвердого тела, обозначая через v скорость, одинаковую для всех точек тела, найдем согласно формуле (3.85): 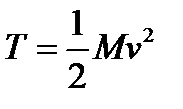 , где через М обозначена масса тела. В случае вращения тела вокруг неподвижной оси Oz, обозначая угловую скорость через
, где через М обозначена масса тела. В случае вращения тела вокруг неподвижной оси Oz, обозначая угловую скорость через 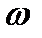 и расстояние элементарной массы
и расстояние элементарной массы 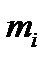 от оси вращения через
от оси вращения через 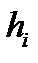 , имеем:
, имеем: 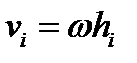 , и формула (3.84 дает:
, и формула (3.84 дает:
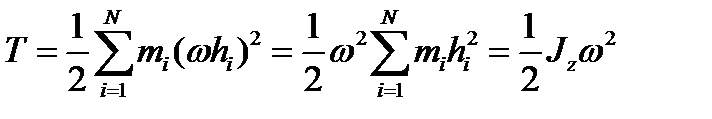 , (3.89)
, (3.89)
где 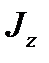 - момент инерции тела относительно оси вращения.
- момент инерции тела относительно оси вращения.
В случае плоского движения твердого тела относительным движением по отношению к поступательно движущимся осям является вращение тела с его угловой скоростью 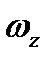 . Поэтому, поместив начало поступательно движущейся системы в центр инерции тела С, можем применить для вычисления величины
. Поэтому, поместив начало поступательно движущейся системы в центр инерции тела С, можем применить для вычисления величины 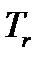 , входящей в выражение (3.88), только что полученную формулу (3.89):
, входящей в выражение (3.88), только что полученную формулу (3.89):
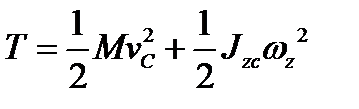
где 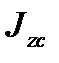 - момент инерции тела относительно оси, перпендикулярной к плоскости движения и проходящей через центр инерции. Эту формулу можно преобразовать к виду, более удобному для некоторых приложений. Напомним, что
- момент инерции тела относительно оси, перпендикулярной к плоскости движения и проходящей через центр инерции. Эту формулу можно преобразовать к виду, более удобному для некоторых приложений. Напомним, что 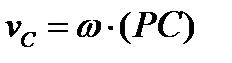 , где PC — расстояние между мгновенным центром скоростей Р и центром инерции С. Тогда получим
, где PC — расстояние между мгновенным центром скоростей Р и центром инерции С. Тогда получим
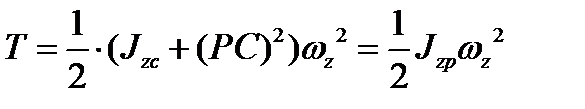
Так как мгновенный центр меняет в процессе движения свое положение, совпадая с различными точками фигуры, то отрезок PC изменяет свою длину, зависящую от положения фигуры, т. е. 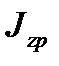 не является постоянной величиной.
не является постоянной величиной.
Переходим к вычислению кинетической энергии твёрдого тела. Удвоенное значение кинетической энергии твёрдого тела представляется интегралом 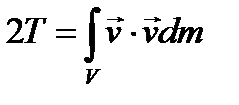 . Подставив в эту формулу скорость точки твёрдого тела
. Подставив в эту формулу скорость точки твёрдого тела 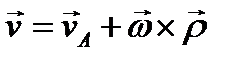 , после некоторых простых преобразований получим
, после некоторых простых преобразований получим
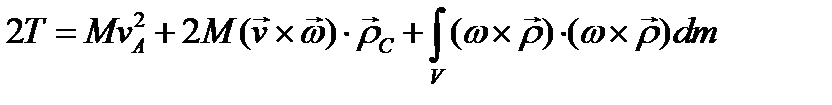 (3.90)
(3.90)
Для вычисления последнего интеграла произведём преобразование подынтегрального выражения, рассматривая его как скалярно-векторное произведение трех векторов: 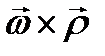 ,
, 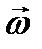 и
и 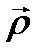 ; произведя круговую перестановку сомножителей в нём и раскрывая при этом двойное векторное произведение, используем далее единичный тензор
; произведя круговую перестановку сомножителей в нём и раскрывая при этом двойное векторное произведение, используем далее единичный тензор 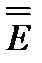 и формулу (3.39)
и формулу (3.39)
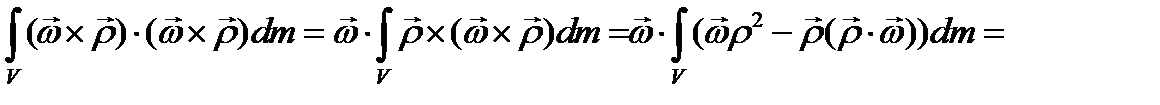
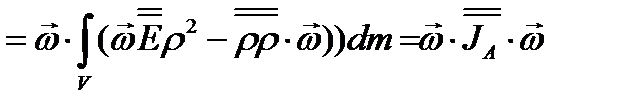
Подставляя этот результат в формулу (3.90), находим окончательное выражение для кинетической энергии твёрдого тела в самом общем случае движения
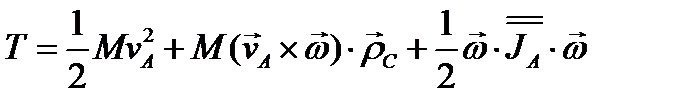
Дата добавления: 2019-12-09; просмотров: 633;











