Изотермический процесс
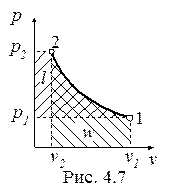 Дано: параметры начального состояния p1, v1, давление конечного состояния p2 (p2 > p1).
Дано: параметры начального состояния p1, v1, давление конечного состояния p2 (p2 > p1).
Определить: недостающие термические параметры T1 и v2, работу и теплоту процесса (w, l, q).
Изотермический процесс, построенный на основании исходных данных (p1, v1, p2) в диаграммах p-v и T-s, представлен на рис. 4.7 и 4.8.
Из уравнения состояния для точки 1 определяет-
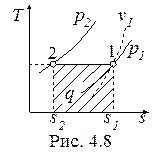 ся температура T = p1.v1/R. Сравнение уравнений состояния для точек 1 и 2 при условии T1 = T2 = T = const (p1.v1 = RT, p2.v2 = RT) дает связь между давлением и объемом в изотермическом процессе:
ся температура T = p1.v1/R. Сравнение уравнений состояния для точек 1 и 2 при условии T1 = T2 = T = const (p1.v1 = RT, p2.v2 = RT) дает связь между давлением и объемом в изотермическом процессе:
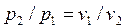 , ,
| (4.38) |
из которой можно определить удельный объем v2.
Формулы для расчета работы и теплоты изотермического процесса получены на основании уравнений:
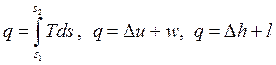 . .
|
Для идеального газа при T = const имеем
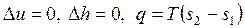 , ,
| (4.39) |
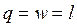 , ,
| (4.40) |
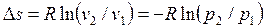 . .
|
Для расчета теплоты (работы) изотермического процесса можно использовать формулы
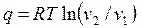 , ,
| (4.41) |
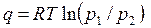 . .
| (4.42) |
Работа и теплота изотермического процесса в p-v- и T-s- диаграммах представлена заштрихованными площадями. Равенство работ w и l подтверждается симметрией изотермы относительно осей координат. Работа процесса w < 0, т.к. v2 < v1; работа l < 0, поскольку p2 > p1; теплота отводится (q < 0), т.к. s2 < s1.
Адиабатный процесс
Адиабатным называется процесс, который протекает без теплообмена с окружающей средой (dq = 0).
В обратимых адиабатных процессах энтропия не изменяется (ds = 0,
s = const), в необратимых - энтропия увеличивается (ds > 0).
Уравнение обратимого адиабатного процесса имеет вид
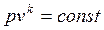 , ,
| (4.43) |
где k – показатель адиабаты.
Для идеального газа
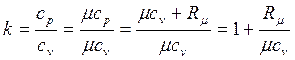 . .
| (4.44) |
Для одноатомного идеального газа показатель адиабаты не зависит от температуры:
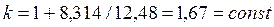 . .
|
Для двух-, трех- и многоатомных идеальных газов k = f(T), т.к. теплоемкость mcv =f(T). С увеличением температуры показатель адиабаты убывает.
Если принять теплоемкость постоянной в соответствии молекулярно-кинетической теорией газов, то для двухатомных газов
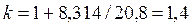 , ,
|
для трех- и многоатомных газов:
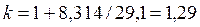 . .
|
Расчет адиабатных процессов двух-, трех- и многоатомных газов при значениях показателя адиабаты 1,4; 1,29 является приближенным, т.к. не учитывает зависимость теплоемкости от температуры.
Совместное решение (4.43) с уравнением состояния идеального газа
pv = RT дает следующие связи параметров:
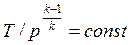 , ,
| (4.45) |
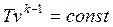 . .
| (4.46) |
Для адиабатного процесса 1-2, в котором параметры изменяются от p1, v1, T1 до p2, v2, T2, на основании уравнений (4.43), (4.45), (4.46) можно получить следующие соотношения между параметрами:
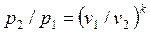 , ,
| (4.47) |
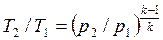 , ,
| (4.48) |
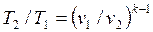 . .
| (4.49) |
Совместное решение уравнений
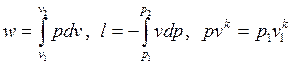
позволяет получить расчетные формулы для работы адиабатного процесса
1-2:
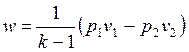 , ,
| (4.50) |
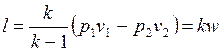 . .
| (4.51) |
С учетом уравнения состояния pv = RT, а также соотношения (4.48) формулу (4.50) можно представить следующим образом:
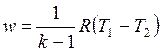 , ,
| (4.52) |
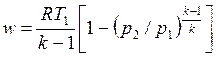 . .
| (4.53) |
По формулам (4.46) - (4.53) производят расчеты адиабатных процессов одноатомного идеального газа и приближенные расчеты двух-, трех- и многоатомных газов при значениях k = 1,4, k = 1,29.
Расчет адиабатных процессов с учетом зависимости k = f(T) по вышеприведенным формулам прост, если известны температуры T1 и T2. В противном случае используется метод последовательных приближений, что значительно усложняет расчет.
Более простым является табличный метод расчета адиабатного процесса идеального газа с учетом зависимости теплоемкости от температуры. В основе расчета лежат следующие уравнения:
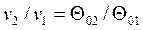 , ,
| (4.54) |
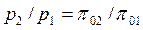 , ,
| (4.55) |
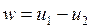 , ,
| (4.56) |
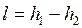 . .
| (4.57) |
Здесь 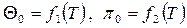 - безразмерные величины, приведенные в таблицах термодинамических свойств газов [7], h, u - табличные значения параметров.
- безразмерные величины, приведенные в таблицах термодинамических свойств газов [7], h, u - табличные значения параметров.
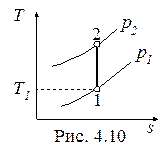
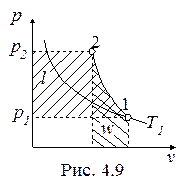 |
Обратимый адиабатный процесссжатия идеального газа, построенный по исходным параметрам p1, T1, p2 в p-v- и T-s- диаграммах, представлен на рис.4.9 и 4.10.
В p-v- диаграмме адиабата - несимметричная гипербола располагается круче изотермы, в T-s- диаграмме – изоэнтропа (s = const, q = 0).
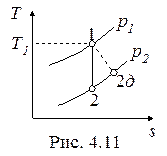 | 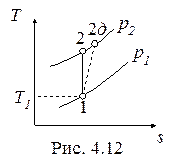 | ||
Необратимые адиабатные процессы (1-2д), протекающие с увеличением энтропии, показаны на рис. 4.11, 4.12.
Работа необратимого адиабатного расширения (рис.4.11) равна
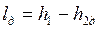 , ,
|
и она меньше работы обратимого процесса, вычисляемого по формуле
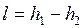 . .
|
Напротив, работа необратимого адиабатного сжатия (рис. 4.12), равная
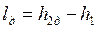 , ,
|
больше работы обратимого процесса
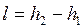 . .
|
Дата добавления: 2021-07-22; просмотров: 576;











