Политропные процессы

Политропные процессы описываются уравнением

,

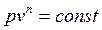(4.58)

где n – показатель политропы, который не зависит от температуры (n = const) и изменяется в пределах от -µ до µ.

Внешняя схожесть уравнений (4.43) и (4.58) позволяет записать расчетные формулы политропного процесса, аналогичные адиабатному:

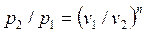,	(4.59)
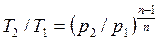,	(4.60)
,	(4.61)
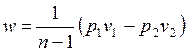,	(4.62)
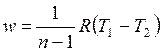,	(4.63)
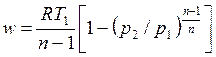,	(4.64)
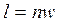.	(4.65)

Теплота политропного процесса рассчитывается по уравнению

,

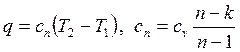(4.66)

где c_n – теплоемкость политропного процесса.

Все многообразие процессов можно описать политропой с показателем -µ < n < µ. Изохорный, изобарный, изотермический, адиабатный процессы являются частным случаем политропных процессов с определенным показателем n. Подставляя конкретные его значения в формулы (4.58) и (4.66), можно доказать, что при:

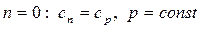- процесс изобарный;

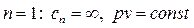- процесс изотермический;

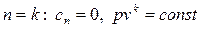- процесс адиабатный;

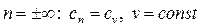- процесс изохорный.

На рис. 4.13 и 4.14 в p-v- и T-s- диаграммах представлено все множество политропных процессов с показателем n, изменяющиxся от -µ до µ.

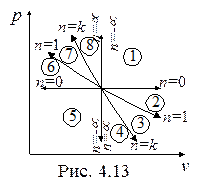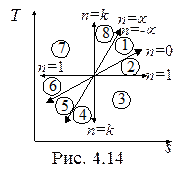Можно выделить следующие группы процессов:

1. Процессы расширения (dv > 0, dw > 0)- области 1, 2, 3, 4.

2. Процессы сжатия (dv < 0, dw < 0) – области 5, 6, 7, 8.

3. Процессы подвода теплоты (ds > 0, dq > 0) – области 8, 1, 2, 3.

4. Процессы отвода теплоты (ds < 0, dq < 0) - области 4, 5, 6, 7.

5. Процессы, протекающие с увеличением температуры (dT > 0, du > 0, dh > 0) - области 7, 8, 1, 2.

6. Процессы, протекающие с уменьшением температуры (dT < 0, du < 0, dh <0) - области 3, 4, 5, 6.

7. Процессы с отрицательной теплоемкостью (c_n < 0, 1 < n < k) - области 3, 7.

В области 3 при подводе теплоты (dq > 0) температура, внутренняя энергия, энтальпия уменьшаются (dT < 0, du < 0, dh < 0). В области 7 при отводе теплоты (dq < 0) температура, внутренняя энергия, энтальпия увеличиваются (dT > 0, du > 0, dh > 0). Это может быть только при отрицательной теплоемкости. В процессах с отрицательной теплоемкостью 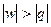, поэтому на производство работы при расширении тратится не только подводимая теплота, но и часть внутренней энергии рабочего тела, а затрачиваемая работа на сжатие компенсирует не только отводимую теплоту, но и повышает внутреннюю энергию рабочего тела.

При изображении политропных процессов в диаграммах p-v и T-s необходимо определить область, к которой они принадлежат, путем сравнения показателя политропы с n = k, n =1 и т.д.

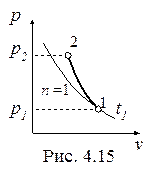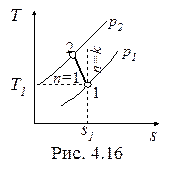Политропный процесс газа с показателем 1<n<k, построенный по исходным параметрам p₁, t₁, p₂ (p₂ > p₁) в p-v- и T-s- диаграммах представлен на рис. 4.15 и 4.16.

В p-v- диаграмме политропа – несимметричная гипербола, которая располагается круче изотермы, т.к. n >1.

В T-s- диаграмме политропа - логарифмическая кривая, которая располагается между изотермой и изоэнтропой, т.к. 1< n < k.