Интегрирование тригонометрических выражений.
Пусть рассматриваются интегралы типа 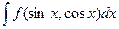 . Если там есть ещё и зависимость от
. Если там есть ещё и зависимость от 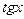 или
или 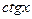 , то всё равно их можно записать через синус и косинус, поэтому можем считать, что вид именно такой: именно
, то всё равно их можно записать через синус и косинус, поэтому можем считать, что вид именно такой: именно 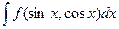
Универсальная тригонометрическая подстановка и её применение.
Замена 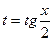 называется универсальной тригонометрической подстановкой. Она иногда приводит к громозким вычислениям, зато универсальна. При этой замене:
называется универсальной тригонометрической подстановкой. Она иногда приводит к громозким вычислениям, зато универсальна. При этой замене:
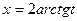 ,
, 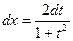 ,
, 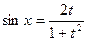 ,
, 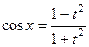 .
.
Докажем формулы, по которым преобразуются синус и косинус.
Можно 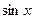 записать по формуле двойного угла, рассматриввая целый угол как удвоенный половинный:
записать по формуле двойного угла, рассматриввая целый угол как удвоенный половинный:
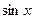 =
= 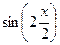 =
= 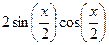 чтобы всё выразилось через
чтобы всё выразилось через 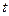 , которое равно
, которое равно 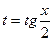 желательно добиться того, чтобы синус и косинус половинного угла делились друг на друга. Для этого мы можем поделить и домножить на косинус ещё раз:
желательно добиться того, чтобы синус и косинус половинного угла делились друг на друга. Для этого мы можем поделить и домножить на косинус ещё раз:
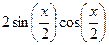 =
= 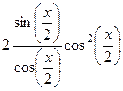 =
= 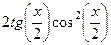 .
.
Вспомним, что 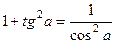 , тогда далее получается
, тогда далее получается
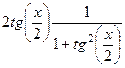 =
= 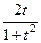 .
.
Аналогично 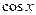 =
= 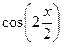 =
= 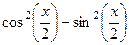 =
=
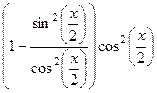 =
= 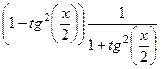 =
= 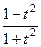 .
.
Пример. Вычислить интеграл. 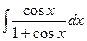 .
.
Решение. 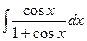 =
= 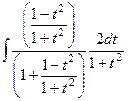 .
.
Свели к рациональной дроби. Далее, преобразуем её: 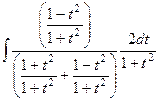 =
= 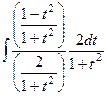 =
= 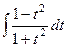 =
=
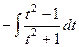 =
= 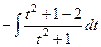 =
= 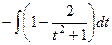 =
=
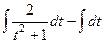 =
= 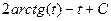 .
.
Сделаем обратную замену, и получим ответ:
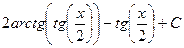 =
= 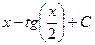 .
.
Как видим, при действии универсальной тригонометрической подстановки могут получаться громоздкие 4-этажные дроби. Поэтому для различных частных случаев, где функция обладает какими-то свойствами чётности, придумали другие подстановки.
Дата добавления: 2017-04-05; просмотров: 1331;











