Доказательство формулы.
Вспомним, что по правилу дифференцирования произведения, которое мы доказывали в прошлом семестре: 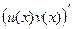 =
= 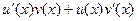 . Тогда
. Тогда 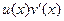 =
= 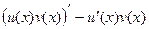 .
.
Тогда и неопределённые интегралы от этих двух функций совпадают:
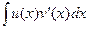 =
= 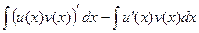 .
.
Но первообразная от производной, это сама функция и есть, т.е.
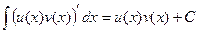 .
.
Поэтому 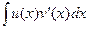 =
= 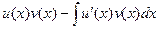 .
.
Пример. Вычислить 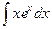 .
.
Решение. Если обозначить 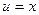 ,
, 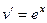 , то при переходе к
, то при переходе к 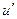 степенной понизится степень, в данном случае она вообще перейдёт в 1. А вот для второго множителя переходим к первообразной, но там не усложняется, остаётся точно так же как и было,
степенной понизится степень, в данном случае она вообще перейдёт в 1. А вот для второго множителя переходим к первообразной, но там не усложняется, остаётся точно так же как и было,  . Поэтому на следующем шаге интеграл содержит вообще не два множителя, а один!
. Поэтому на следующем шаге интеграл содержит вообще не два множителя, а один!
Составим таблицу:
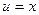
| 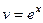
|
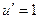
| 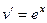
|
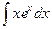 =
= 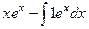 , тогда получаем ответ:
, тогда получаем ответ: 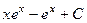 .
.
Пример.Вычислить интеграл: 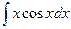 Составим таблицу:
Составим таблицу:
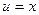
| 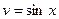
|
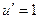
| 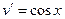
|
После применения формулы, останется интеграл, в котором всего лишь один множитель, а не два, потому что 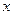 переходит в 1, и один из множителей исчезает.
переходит в 1, и один из множителей исчезает.
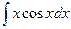 =
= 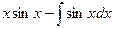 =
= 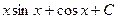 .
.
А есть такие случаи, когда функция состоит не из 2 множителей, а всего из одного, но мы ведь всё равно можем считать, что второй множитель есть, только он равен 1.
Пример. 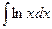 .
.
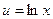
| 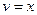
|
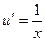
| 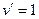
|
Здесь производная от подынтегральной функции устроена лучше и проще, чем сама функция, но правда, пришлось допустить некоторое незначительное усложнение типа функции при переходе от 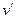 к
к 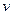 .
.
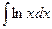 =
= 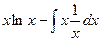 =
= 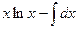 =
= 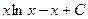 .
.
Дата добавления: 2017-04-05; просмотров: 1350;











