Движение взвешенных наносов
Перенос тяжелых твердых частиц турбулентным потоком во взвешенном состоянии становится возможным тогда, когда средняя величина вертикальных пульсационных скоростей начинает превосходить гидравлическую крупность частиц. Средние значения вертикальных пульсационных скоростей близки к значениям динамической скорости 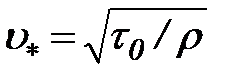 . Таким образом, приближенным условием переноса твердых частиц во взвешенном состоянии может служить неравенство
. Таким образом, приближенным условием переноса твердых частиц во взвешенном состоянии может служить неравенство 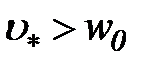 .
.
Отношение объема твердых частиц к выделенному общему объему жидкости и частиц
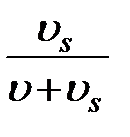 .
.
называется объемной концентрацией наносов.
Отношение массы твердых частиц к тому же общему объему
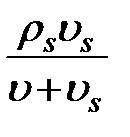 .
.
называется массовой концентрацией, или мутностью. Если поперечные размеры твердых частиц малы по сравнению с поперечными размерами потока, то в написанных выражениях можно перейти к пределу, получая значение концентрации в точке. Так, для объемной концентрации будем иметь
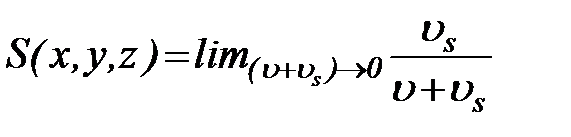 . (80)
. (80)
Массовая концентрация в точке будет 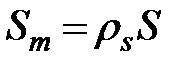 . Объемная концентрация представляет собой безразмерную величину. Массовая концентрация выражается в килограммах на кубический метр (кг/м3). В гидрологии ее часто выражают в граммах на кубический метр (г/м3). Так же как скорость течения, концентрация наносов в каждой точке турбулентного потока пульсирует. Дальше мы будем заниматься только осредненными значениями концентрации. Распределение осредненной концентрации наносов на вертикали не равномерно: от свободной поверхности к дну концентрация всегда возрастает. Чем крупнее взвешенные частицы, тем это возрастание резче.
. Объемная концентрация представляет собой безразмерную величину. Массовая концентрация выражается в килограммах на кубический метр (кг/м3). В гидрологии ее часто выражают в граммах на кубический метр (г/м3). Так же как скорость течения, концентрация наносов в каждой точке турбулентного потока пульсирует. Дальше мы будем заниматься только осредненными значениями концентрации. Распределение осредненной концентрации наносов на вертикали не равномерно: от свободной поверхности к дну концентрация всегда возрастает. Чем крупнее взвешенные частицы, тем это возрастание резче.
Элементарный массовый расход взвешенных наносов выражается интегралом
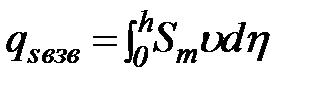 (81)
(81)
Произведение Smuназывается единичным расходом наносов. Примерный вид эпюр концентрации и единичных расходов показан на рис. 42.
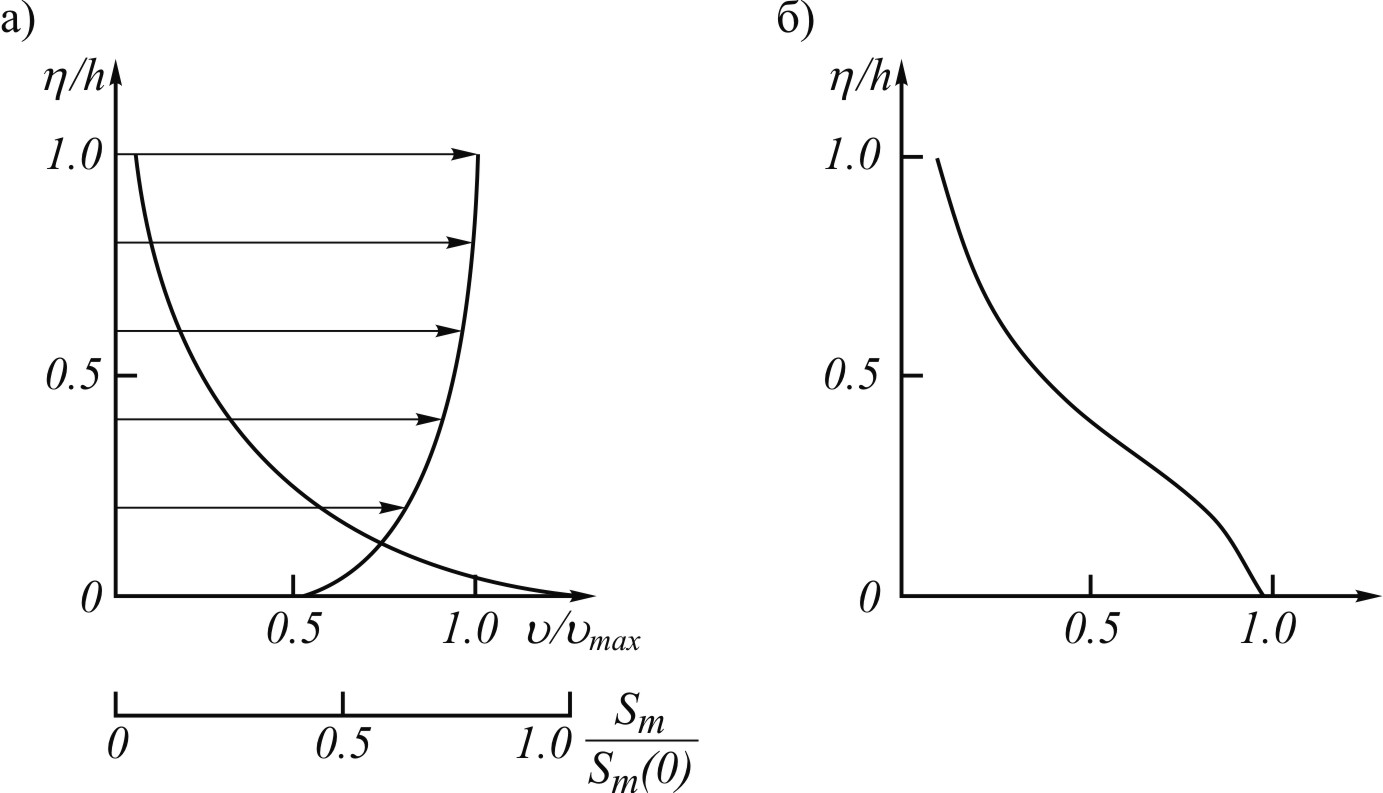
Рис. 42. Эпюры скоростей течения и мутности (а)
и единичных расходов наносов (б)
Чтобы получить полный массовый расход взвешенных наносов в поперечном сечении потока, надо выражение элементарного расхода (81) проинтегрировать по ширине русла:
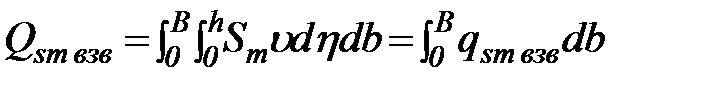 . (82)
. (82)
Разделив элементарный расход наносов на элементарный расход, воды и весь расход наносов на полный расход воды, получим величины средней концентрации наносов (среднюю мутность), соответственно, на вертикали и в живом сечении:
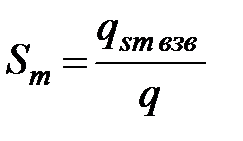 , (83)
, (83)
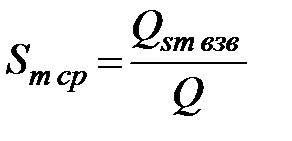 . (84)
. (84)
Остановимся на физической стороне транспорта взвешенных наносов. Рассмотрим прямолинейный равномерный поток, несущий взвешенные твердые частицы, и найдем условие, при котором в этом потоке может существовать установившееся, т.е. не изменяющееся во времени, распределение концентрации наносов по вертикали. Вертикальные перемещения твердых частиц происходят вследствие двух причин: действия на частицы силы тяжести и действия на них беспорядочного движения турбулентных вихрей.
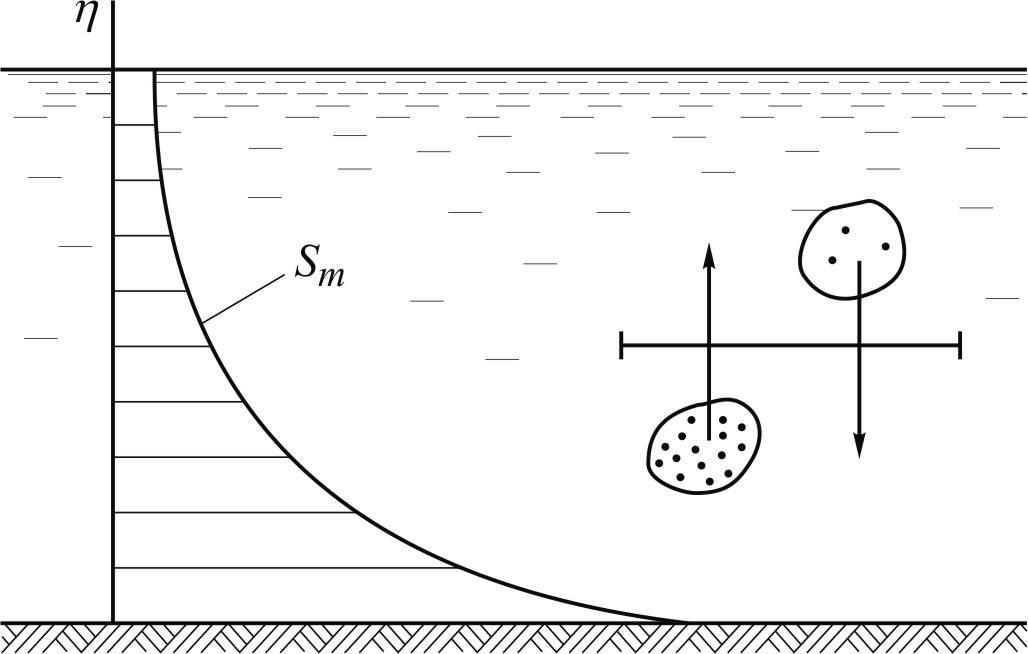 Рис. 43. Схема диффузионного переноса частиц
наносов по вертикали
Рис. 43. Схема диффузионного переноса частиц
наносов по вертикали
|
Таким образом, турбулентное перемешивание создает результирующий перенос массы наносов снизу вверх – из области высокой концентрации наносов в область низкой концентрации. Плотность этого потока массы выражается аналогично тому, как выражается плотность потока тепла, а именно
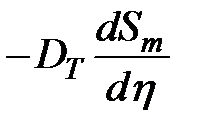 ,
,
где: DT – коэффициент турбулентной диффузии.
Знак минус перед этим выражением показывает, что поток массы направлен в сторону убывания концентрации.
Таким образом, мы имеем два вертикальных потока массы: гравитационный, направленный сверху вниз, и диффузионный, направленный снизу вверх. Для того чтобы распределение концентрации по вертикали не изменялось, необходимо чтобы плотности двух этих противоположно направленных потоков были равны:
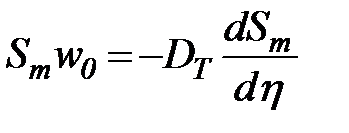 . (85)
. (85)
Уравнение (85) позволяет найти закон установившегося распределения концентрации.
Разделяя в этом уравнении переменные, интегрируя в пределах от некоторого фиксированного значения 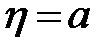 до текущего h и освобождаясь от логарифмов, получаем такой закон в виде
до текущего h и освобождаясь от логарифмов, получаем такой закон в виде
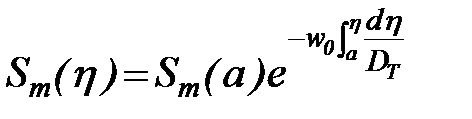 . (86)
. (86)
Если допустить, что коэффициент диффузии DT на вертикали не изменяется, то формула (84) переходит в простую зависимость, полученную В. Шмидтом,
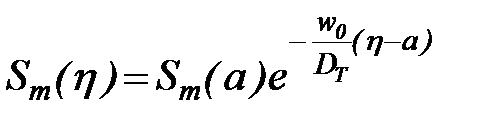 . (87)
. (87)
В действительности коэффициент турбулентной диффузии значительно меняется по вертикали. Закон его изменения такой же, как у коэффициента турбулентной теплопроводности kT и других аналогичных коэффициентов, характеризующих способность турбулентного потока к поперечному (вертикальному) переносу различных субстанций. Этот закон может быть найден с помощью логарифмического распределения скоростей.
Он записывается так:
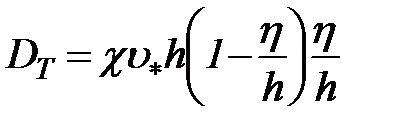 , (88)
, (88)
где: c – параметр Кармана;
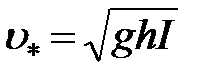 – динамическая скорость.
– динамическая скорость.
Формула (88) показывает, что коэффициент диффузии достигает максимума на середине вертикали, а при приближении к свободной поверхности и ко дну убывает до нуля.
Подставив выражение DT по формуле (88) в уравнение (86) и интегрируя, получаем следующее распределение концентрации взвешенных наносов по вертикали:
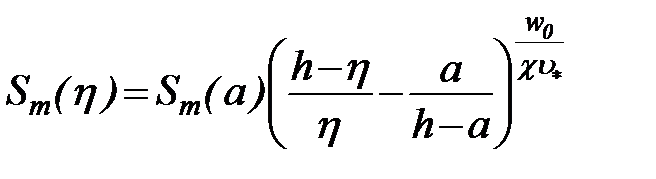 . (89)
. (89)
Чтобы рассчитать распределение концентрации по формуле (89), надо знать величину концентрации в точке вертикали, где 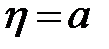 . Эта точка, т.е. высота а, на которой концентрация должна быть измерена, может выбираться произвольно, однако для обеспечения надежных результатов следует назначать ее в нижней части вертикали, где концентрация наносов достаточно велика. Если наносы неоднородные (а в реках это всегда так), то расчет по формуле (89) надо выполнять для отдельных фракций наносов. Полная концентрация получается путем сложения частных, пофракционных концентраций.
. Эта точка, т.е. высота а, на которой концентрация должна быть измерена, может выбираться произвольно, однако для обеспечения надежных результатов следует назначать ее в нижней части вертикали, где концентрация наносов достаточно велика. Если наносы неоднородные (а в реках это всегда так), то расчет по формуле (89) надо выполнять для отдельных фракций наносов. Полная концентрация получается путем сложения частных, пофракционных концентраций.
Тщательно выполненные опыты в лабораторных лотках свидетельствуют о высокой точности уравнения (89). Не так благополучно обстоит дело в естественных потоках. Вследствие неравномерного движения воды, неровностей дна и случайных колебаний состава донных частиц распределение концентрации может здесь заметно отклоняться от теоретического. Наряду с этим только расчет по теоретической зависимости позволяет получить значения концентрации в непосредственной близости ко дну – там, где поместить измерительный прибор невозможно. Поэтому практическое значение формулы (89) все же очень велико.
Сток наносов
Суммарный годовой сток взвешенных наносов рек земного шара, впадающих в Мировой океан, составляет внушительную цифру – 15,7 млрд. т. В объемном выражении это равно 5,9 млрд. м3 (в плотном теле). Если разделить последнюю цифру на площадь океанических склонов континентов (т.е. площадь суши за вычетом площади областей внутреннего стока) 105 млн. км2 и учесть пористость грунта, то получится, что за счет смыва грунта дождевыми и талыми водами поверхность океанических склонов понижается за год в среднем на 0,1 мм.
Толщина среднего годового слоя смыва грунта сильно колеблется по поверхности суши. Ее росту способствуют обильные осадки, пересеченный рельеф местности, рыхлое строение грунта. Наименьшая эрозия наблюдается в равнинных бассейнах, сложенных ледниковыми отложениями и хорошо облесенных.
Сильно изменчивой оказывается и концентрация взвешенных наносов в водах разных рек. У рек северо-западной части ETC, и на севере Западно-Сибирской низменности средняя годовая мутность очень мала – она составляет менее 25 г/м3. Реки лесной зоны ETC имеют среднюю мутность от 25 до 50 г/м3. Далее к югу средняя годовая мутность речных вод возрастает и в степной зоне достигает 100-250 г/м3, а местами и выше. На большей части территории Сибири средняя мутность воды в реках составляет 25-50 г/м3. Повышенную мутность имеют здесь реки предгорий Алтая и реки Казахстана.
В Средней Азии очень высокой мутностью отличается река Амударья – около 3500 г/м3. Наибольшие значения средней мутности на территории СССР встречаются у некоторых горных рек Кавказа. Рекорд здесь держит протекающая в восточной части Кавказского хребта р. Аксай, со средней годовой мутностью 11700 г/м3.
Значения среднего годового стока взвешенных наносов некоторых рек СССР приведены в табл. 7.
Таблица 7
Сток взвешенных наносов некоторых рек СССР (по Г. И. Шамову)
| Река | Створ | Площадь бассейна, км2 | Средний годовой сток наносов, млн. т | Средняя мутность, г/м3 |
| Большая Северная Двина | Архангельск | 360 000 | 10.0 | |
| Волга | Дубовка | 1 350 000 | 25.6 | |
| Ока | Новинки | 245 000 | 3.0 | |
| Днепр | Киев | 328 000 | 1.8 | |
| Кубань | Краснодар | 45 900 | 8.2 | |
| Кура | Тбилиси | 21 100 | 11.2 | |
| Обь | Салехард | 2 450 000 | 12.9 | |
| Иртыш | Тобольск | 956 000 | 11.1 | |
| Енисей | Игарка | 2 470 000 | 16.6 | |
| Амударья | Керки | 227 000 |
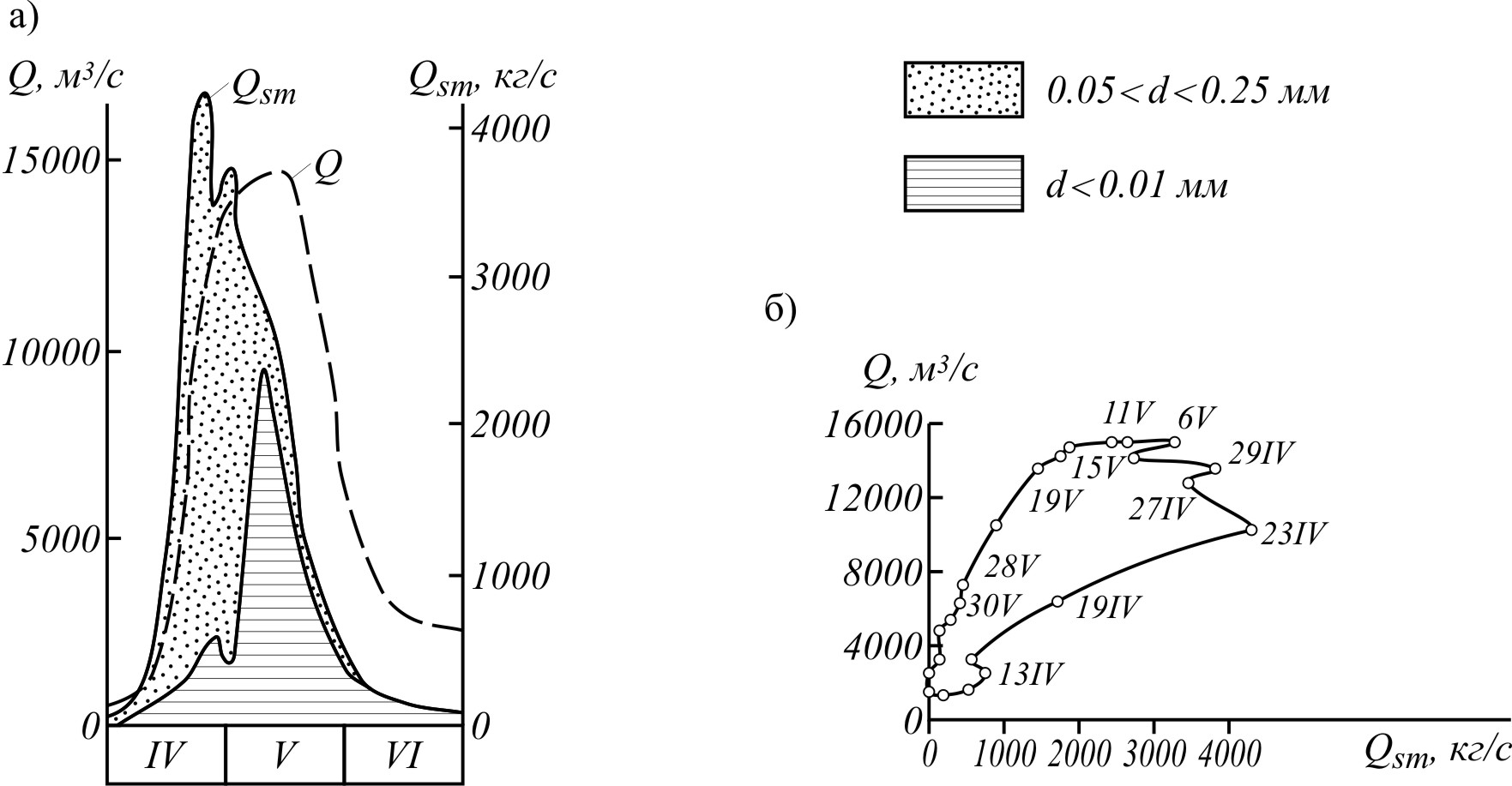 Рис. 44. Графики колебания расходов воды и расходов взвешенных наносов (а) и график связи расходов воды и расходов наносов (б) на р. Каме у с. Сокольи Горы за 1938 г. (по Г.И. Шамову)
Рис. 44. Графики колебания расходов воды и расходов взвешенных наносов (а) и график связи расходов воды и расходов наносов (б) на р. Каме у с. Сокольи Горы за 1938 г. (по Г.И. Шамову)
|
Сток влекомых наносов менее изучен, чем сток взвешенных наносов. У равнинных рек он обычно составляет не более 3-5% от стока взвешенных наносов. Однако при переходе к горным рекам это соотношение резко меняется. У горных рек, имеющих большие уклоны, сток влекомых наносов может превосходить сток взвешенных.
В моря и океаны влекомых наносов поступает мало. На приустьевых участках впадающих в них рек расходы влекомых наносов нередко бывают меньше, чем на вышележащих участках. Это связано с тем, что в транспорте влекомых наносов, всегда имеющих русловое происхождение, главное место занимает не транзитный перенос, а процесс переотложения, т.е. захвата частиц потоком на одном участке русла и их аккумуляции на другом. Таким путем идет обмен наносами между руслом и поймой. Частицы грунта, поступившие в русло в результате размыва берега и пополнившие здесь расход влекомых наносов, откладываются ниже на побочнях или осередках и по истечении нескольких лет или десятков лет снова входят в состав поймы.
Расходы взвешенных, и влекомых наносов и мутность воды испытывают сильные колебания внутри года. На реках СССР, имеющих снеговые половодья, максимум расхода взвешенных наносов обычно приходится на время подъема уровней, когда идет наиболее интенсивное стекание воды со склонов бассейна. В формировании этого максимума участвуют преимущественно мелкие илистые и глинистые частицы (крупностью менее 0,01 мм). Более крупные частицы, захватываемые потоком в русле, начинают двигаться позднее и максимумы частного расхода взвешенных наносов песчаной фракции совпадают по времени с пиком паводка. В это же время наблюдаются и максимальные расходы влекомых наносов. На спаде паводка расходы наносов всех фракций резко уменьшаются.
В виде иллюстрации к сказанному на рис. 44, а) приведены графики колебания расхода воды и расходов наносов двух фракций на р. Каме у
с. Сокольи Горы за 1938 г. (до постройки каскада Камских водохранилищ). На рис. 44, б) приведен построенный по этим же измерениям график связи расходов воды и расходов взвешенных наносов. Как видно на графике, эта связь резко неоднозначна: одному и тому же расходу воды в фазе подъема отвечает гораздо больший расход взвешенных наносов, чем в фазе спада. Причина этой неоднозначности очевидна: мелкие частицы, смываемые водой со склонов бассейна, легко транспортируются рекой и их количество в реке зависит не от скорости течения, а от интенсивности смыва на склонах и условий добегания воды с наносами от места смыва до речной сети.
Несколько лучше обстоит дело со связью между расходами воды и расходами влекомых наносов, которые прямо зависят от скорости течения. Однако и здесь однозначности нет. Последнее объясняется сложными переформированиями донных гряд при прохождении паводка. На подъеме высоты и длины гряд сначала растут, затем рост гряд в высоту прекращается, и если русловые наносы при больших расходах воды энергично взвешиваются, то высота гряд может уменьшиться вплоть до нуля. На спаде грядовый рельеф восстанавливается, снова формируются большие гряды, которые далее, вследствие падения скоростей, переформировываются медленно. Таким образом, перестройка грядового рельефа дна отстает от изменений стока. В результате при одном и том же расходе воды на спаде паводка в реке наблюдаются гряды, которые имеют крупные размеры, но движутся медленнее, чем на подъеме. Расходы влекомых наносов также оказываются меньшими.
Изложенное в этой главе показывает, что транспорт наносов в реках представляет собой очень сложное, многостороннее явление. Изучению этого явления посвящено много теоретических, лабораторных и полевых исследований. Наибольшее практическое значение имеет транспорт русловых наносов, так как им определяются деформации речных русл: изменения размеров и формы поперечных сечений потока, изменения плановой конфигурации русел. Такие деформации идут естественным путем и возникают в результате человеческой деятельности. Прогноз русловых деформаций стал в настоящее время одной из важных составных частей гидротехнического проектирования Для его составления требуются обширные исходные данные и расчетный аппарат, опирающийся на теорию движения наносов.
В связи с серьезностью задач этого рода и в результате накопления исследовательских данных круг вопросов, охватывающих движение воды в реках, транспорт наносов и русловые деформации, с середины текущего столетия выделился в специальную дисциплину – динамику русловых потоков.
Дата добавления: 2017-04-05; просмотров: 3231;











