Физико-механические свойства наносов
Частицы грунта, перемещаемые водой в реках, озерах, водохранилищах и морях, называются наносами. Речные потоки либо захватывают эти частицы со своего дна и берегов, либо получают их в результате смыва почв с поверхности бассейна. Наносы первого рода называются русловыми, второго рода – внерусловыми. В конечном итоге и те и другие являются продуктами разрушения изверженных и осадочных горных пород.
Плотность частиц наносов меняется в довольно узких границах 2500-2800 кг/м3. В расчетах пользуются средним значением плотности
rs= 2650 кг/м3. Ему отвечает удельный вес частиц 26×103 Н/м3. Геометрические размеры частиц, напротив, изменяются крайне широко – от тысячных долей миллиметра до десятков сантиметров. Этот диапазон делится на ряд интервалов, называемых фракциями грунта.
В качестве линейного размера частиц используется диаметр d равновеликого шара. Значения d, мм, отвечающие границам фракций, следующие:
Валуны...................... >100
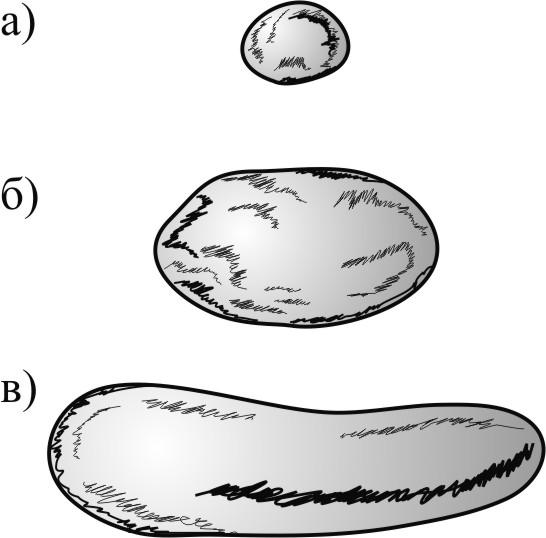 Рис. 38. Частицы наносов
Рис. 38. Частицы наносов
|
Гравий крупный........ 10-5
средний........ 5-2
мелкий........ 2-1
Песок крупный........ 1,0-0,5
средний........ 0,5-0,2
мелкий........ 0,2-0,1
Пыль.......................... 0,1-0,01
Ил.............................. 0,01-0,001
Глина......................... <0,001
По своей форме частицы наносов делятся на шарообразные
(рис. 38, а), эллипсоидальные (рис. 38, б) и уплощенные, или пластинчатые (рис. 38, в). Частицы песка и мелкого гравия имеют шарообразную форму, среди частиц среднего и крупного гравия встречается много эллипсоидальных. Частицы гальки обычно уплощенные.
Наносы, так же как донные грунты, представляют собой смеси частиц различной крупности. Неоднородность состава наносов описывается интегральной функцией распределения вероятностей их диаметров:
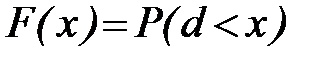 .
.
Такие функции получают эмпирическим путем на основе механического анализа проб наносов. Графическим изображением этих функций служат кривые гранулометрического состава (рис. 39). Степень неоднородности состава наносов выражается коэффициентом вариации диаметров частиц, но в практических расчетах пользуются более простыми показателями неоднородности, чаще всего – отношением медианного диаметра частиц к диаметру, отвечающему вероятности 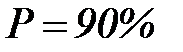 . Значения отношения
. Значения отношения 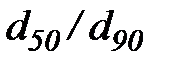 обычно лежат между 0,3 и 0,7.
обычно лежат между 0,3 и 0,7.
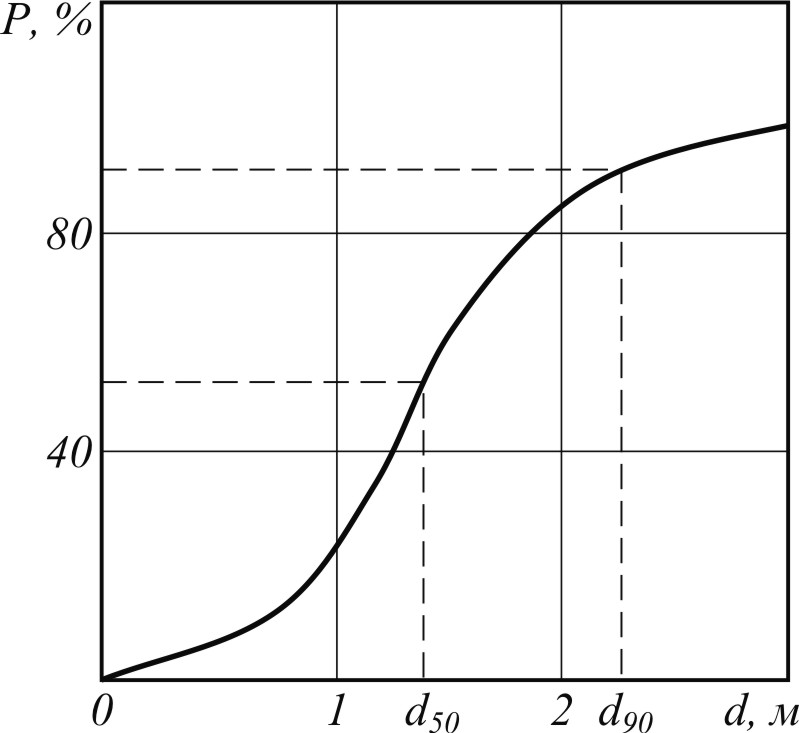 Рис. 39. Кривая
гранулометрического состава
Рис. 39. Кривая
гранулометрического состава
|
В движении взвешенных твердых частиц важную роль играет их гидравлическая крупность. Так называется скорость равномерного падения твердых частиц в покоящейся жидкости. Если опустить тяжелую твердую частицу в жидкость без начальной скорости, она будет падать ускоренно, пока сила сопротивления движению не сравняется с силой избыточного веса частицы. После этого частица будет падать равномерно. Время разгона частиц очень мало, поэтому в расчетах предполагают, что твердые частицы всегда падают относительно окружающей жидкости со скоростью, равной их гидравлической крупности.
Гидравлическая крупность частиц наносов зависит от следующих факторов: ускорения свободного падения g, плотности воды r, плотности частиц rs, коэффициента вязкости воды m, линейного размера частиц d и их формы. Последнюю характеризуют с помощью безразмерного коэффициента формы a. Таким образом, обозначая гидравлическую крупность w0, имеем
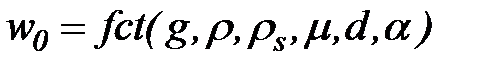 . (73)
. (73)
Величины r и rs при движении наносов в реках почти постоянны. То же относится и к ускорению g. Отсюда следует, что величина w0 фактически изменяется под влиянием только трех факторов: m, d и a. Если же ограничиться классом геометрически подобных частиц, например шарообразными частицами песка и мелкого гравия, то величина w0 станет изменяться в силу изменения только двух независимых переменных: m и d.
Вязкостью жидкости определяются действующие в ней силы внутреннего трения. Чем больше коэффициент вязкости m, тем большее сопротивление движению испытывает падающее в жидкости твердое тело. Вязкость воды связана обратной зависимостью с температурой. Поэтому ранней весной и осенью, когда температура воды низка, а ее вязкость относительно велика, падающие в воде мелкие твердые частицы испытывают большее сопротивление движению и, следовательно, имеют меньшую гидравлическую крупность, чем летом.
Однако вязкость неодинаково влияет на гидравлическую крупность частиц разных размеров. Чем мельче частица, тем сильнее влияет вязкость на ее движение. Для крупных частиц влияние вязкости пренебрежимо мало. Это объясняется тем, что силы вязкости имеют молекулярную природу и проявляются только тогда, когда относительные скорости жидкости малы. Вокруг крупной твердой частицы, падающей в воде с большой скоростью, жидкость движется турбулентно и сопротивление движению частицы определяется уже не вязкостью, а переносом количества движения в перемешивающейся жидкости. Этим общим соображениям можно придать количественный вид, введя число Рейнольдса, в котором характерной скоростью служит гидравлическая крупность твердых частиц, а характерным поперечным размером – их диаметр:
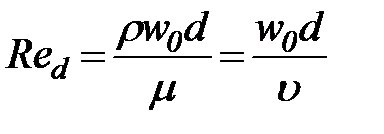 .
.
При значениях числа 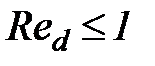 величина гидравлической крупности выражается формулой Стокса
величина гидравлической крупности выражается формулой Стокса
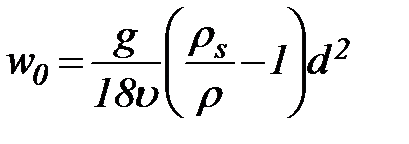 . (74)
. (74)
Как видно из этой формулы, при малых числах Red гидравлическая крупность обратно пропорциональна коэффициенту вязкости. К области этих малых чисел Red относятся частицы с диаметром, меньшим (приблизительно) 0,1 мм. В области чисел Рейнольдса 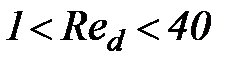 , приблизительно соответствующей диапазону диаметров
, приблизительно соответствующей диапазону диаметров 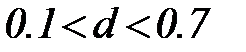 мм, гидравлическая крупность делается обратно пропорциональной u1/3. С дальнейшим увеличением диаметра d влияние вязкости на гидравлическую крупность становится еще более слабым и при
мм, гидравлическая крупность делается обратно пропорциональной u1/3. С дальнейшим увеличением диаметра d влияние вязкости на гидравлическую крупность становится еще более слабым и при 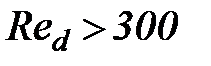 или
или 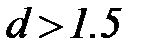 мм исчезает совсем.
мм исчезает совсем.
В таблице 6 приведены значения гидравлической крупности частиц песка и мелкого гравия. Более подробные таблицы приводятся в гидравлических справочниках.
Таблица 6
Гидравлическая крупность частиц песка и мелкого гравия
| d, мм | w0, см/с, при t,ºС | d, мм | w0, см/с, при t,ºС | ||||||
| 0.10 | 0.44 | 0.51 | 0.59 | 0.66 | 1.0 | 10.50 | 10.67 | 10.84 | 11.00 |
| 0.20 | 1.54 | 1.71 | 1.88 | 2.04 | 1.5 | 16.10 | 16.27 | 16.44 | 16.60 |
| 0.50 | 4.90 | 5.07 | 5.24 | 5.40 | 2.0 | 19.00 | 19.00 | 19.00 | 19.00 |
Дата добавления: 2017-04-05; просмотров: 3217;











