Пресноводный лед и закономерности нарастания его толщины

Пресноводный лед представляет собой кристаллическое тело с плотностью r_л = 916 – 918 кг/м³. Удельная теплота плавления льда r_л = 335 Дж/г. Коэффициенты теплопроводности k_л = 2,26 Вт/(м×К). Предел прочности льда на сжатие при температуре 10-15°С составляет 300-400 Н/см². Это лишь немного меньше предела прочности на сжатие поперек волокон сосны и ели.

Толщина ледяного покрова в реках и водоемах регулируется соотношением между количеством тепла, поступающим ко льду от дна или глубинных слоев воды, и количеством тепла, уходящим через лед и снег в атмосферу. Рассмотрим эти процессы подробнее.

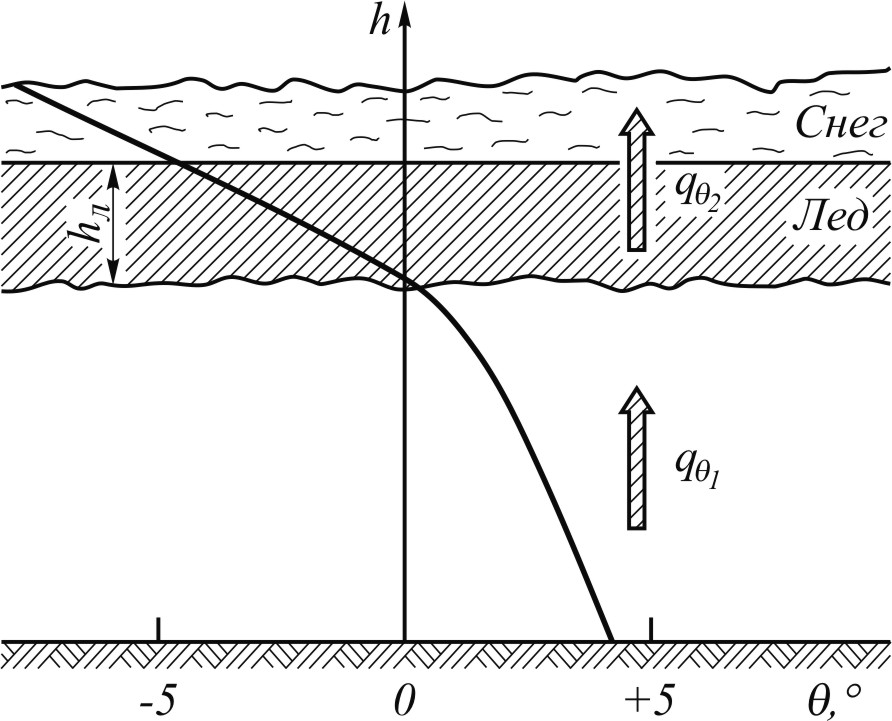Рис. 37. Схема зимнего теплообмена в реках

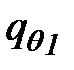Пусть (рис. 37) обозначает плотность потока тепла, проходящего через воду от дна к нижней поверхности ледяного покрова, и 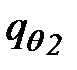– плотность потока тепла через лед и снег. Если 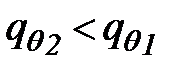, разность этих величин будет идти на таяние льда, а если 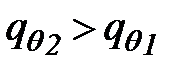– на ледообразование.

Таким образом, для малого промежутка времени dt имеем

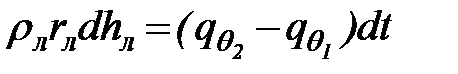, (64)

где: h_л – толщина льда (остальные обозначения были указаны).

Считая распределение температуры поперек ледяного покрова линейным и помня, что температура нижней поверхности льда равна 0°С, градиент температуры во льду найдем, разделив температуру верхней поверхности льда на толщину льда. Если снега на льду нет, то по закону Фурье получим

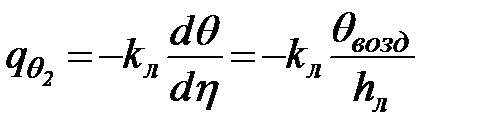, (65)

где: q_возд – температура воздуха.

В качестве грубого, но практически приемлемого допущения принимают, что формула (65) применима и при наличии снегового покрова, если коэффициент k_л заменить в ней некоторым приведенным коэффициентом теплопроводности 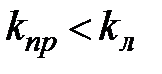. Сделав такую подстановку в формуле (65) и перенеся полученное выражение 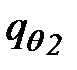в уравнение (64), получим

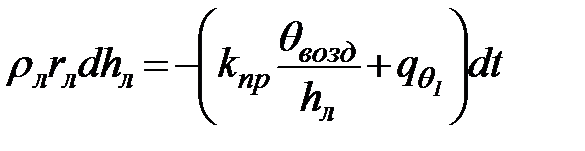. (66)

Наиболее простой закон нарастания толщины льда реализуется в глубоководных водоемах, где турбулентность зимой затухает и поэтому плотностью потока тепла 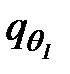можно пренебречь. Положив в уравнение (66) 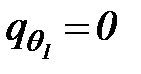и разделив обе его части на 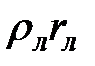будем иметь

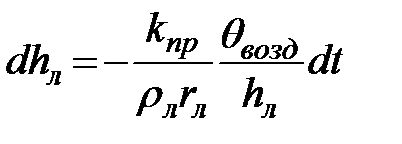. (67)

Обозначив 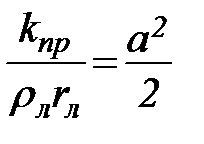и разделив переменные, перепишем (67) в виде

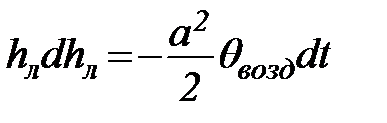. (68)

Интегрируя это уравнение от момента времени 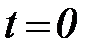, отвечающего началу ледообразования, до некоторого текущего t и приняв во внимание, что 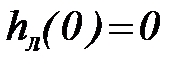, получим

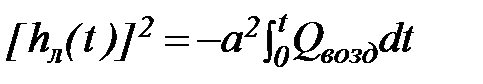, (69)

или окончательно

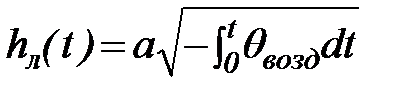. (70)

Пропорциональность толщины льда корню квадратному из интеграла температур воздуха хорошо подтверждается натурными наблюдениями не только в озерах и водохранилищах, но и в реках. В практических расчетах интеграл температур заменяют алгебраической суммой среднесуточных температур. В качестве примера расчетных выражений приведем простую формулу Ф.И. Быдина

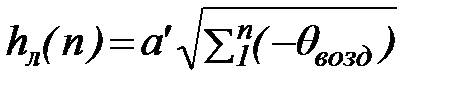, (71)

где: n – число дней от начала ледообразования.

Коэффициент a' на основании натурных наблюдений берется равным при отсутствии снегового покрова 0,037 м/град^1/2 и при наличии снегового покрова 0,02 м/град^1/2.

Раздельный учет теплопроводности льда и снега приводит к уравнению

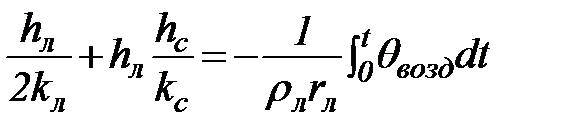, (72)

где: h_c и k_c – соответственно толщина снега и коэффициент его теплопроводности.

Пользование этой формулой затруднено недостатком данных: о толщине и плотности снега (последняя влияет на величину коэффициента k_c).

Интенсивное турбулентное перемешивание воды в реках и его слабость или отсутствие в озерах и водохранилищах приводят к тому, что в течение зимы к нижней поверхности льда в реках подводится больше тепла, чем в озерах и водохранилищах. Вследствие этого толщина льда в реках меньше, чем в озерах и водохранилищах. К концу зимы в реках ETC толщина льда составляет обычно 0,3-0,4 м, а в озерах и водохранилищах около 0,5 м. В условиях сурового климата Сибири толщина льда в реках может достигать 1,0-1,5 м, а малые реки могут промерзать до дна.