Виды питания рек. факторы подстилающей поверхности

Вода, поступающая в виде осадков на поверхность бассейна, попадает в русловую сеть посредством поверхностного (склонного) стекания и фильтрации через грунт. Фильтрация обеспечивает меньшую, но относительно устойчивую слагаемую питания рек. Поверхностное питание может быть трех видов: дождевое, снеговое и ледниковое. Большинство рек СССР имеет смешанное – дождевое и снеговое питание, в котором роль последнего преобладающая. Средние цифры для главных рек СССР таковы: снеговое питание составляет 65-80%, дождевое 15-20% общей величины стока. На долю подземного питания приходится 20-35%.

Ледниковое питание характерно для высокогорных участков рек. Оно создается в результате того, что ледники движутся, а линия нулевых температур изменяет в течение года свое положение по высоте. Когда нижняя оконечность ледника – его язык – располагается ниже линии нулевых температур, лед тает.

На отношение стока реки к выпадающим в бассейне осадкам, т.е. на коэффициент стока, оказывают существенное влияние характер поверхности бассейна и состав грунтов. Еще сильнее эти факторы могут влиять на внутригодовое распределение стока.

Крутые склоны бассейна способствуют быстрому склоновому стеканию и, ограничивая тем самым испарение, обеспечивают высокий коэффициент стока. Неравномерность стока получается при этом тоже высокой. Для горных рек характерны резкие колебания расходов и уровней воды. Этот эффект может усиливаться при малопроницаемых грунтах.

В плоских равнинных бассейнах склоновое стекание идет медленно, в понижениях местности вода может застаиваться и, следовательно, много влаги может теряться на испарение. Малопроницаемые, например глинистые, грунты будут в этом случае способствовать испарению, т.е. снижению коэффициента стока.

Важная роль в процессах стока принадлежит растительному покрову бассейна. Лес оказывает многостороннее влияние на сток. Он увеличивает потери воды за счет повышенного испарения с крон и транспирации (отсасывания грунтовых вод корневыми системами). В то же время он уменьшает испарение с почвы, защищая ее от солнечной радиации. Корневые системы деревьев разрыхляют почву и сильно увеличивают ее водопроницаемость. Суммарный результат получается следующим. В равнинных бассейнах лес способствует увеличению среднего коэффициента стока. Годовой сток с более облесенных бассейнов бывает на 10-40% выше, чем с менее облесенных. Увеличивая грунтовое питание и задерживая весеннее снеготаяние, лес оказывает выравнивающее влияние на внутригодовое распределение стока. Колебания стока в лесных бассейнах имеют более плавный характер, чем в безлесных.

Еще значительнее регулирующее влияние болот. Максимальные расходы дождевых и снеговых паводков могут быть в заболоченных бассейнах в несколько раз меньше, чем в бассейнах такой же площади и с таким же количеством осадков, но имеющих мало болот. Что касается средней величины стока, то в зоне избыточного и достаточного увлажнения, к которой принадлежат северная и центральная части ETC и почти вся Сибирь, влияние болот на нее практически незаметно. Наиболее мощными регуляторами стока являются озера. Яркий пример озерной реки со слабо колеблющимся стоком представляет Нева. Вытекая из Ладожского озера – крупнейшего водоема Европы (площадь зеркала 17970 км²) – и имея в пределах своего бассейна такие крупные озера, как Онежское, Сайменское и Ильмень, она отличается очень малым отношением максимального за многолетний период расхода воды к минимальному – всего лишь около 6. Повышенное испарение с поверхности озер в зоне избыточного и достаточного увлажнения лишь немного снижает величину среднего стока. Картина резко изменяется при переходе к засушливым и полупустынным районам. При достаточно большом отношении площади озера к площади бассейна озеро здесь может испарять всю воду, приносимую его притоками, т.е. может стать бессточным.

1.3. Колебания стока как случайный процесс.
Способы статистического описания стока

В соответствии со сменой времен года речной сток ежегодно проходит один и тот же цикл изменений. Однако даты наступления отдельных фаз колебаний и значения расходов воды в эти фазы в многолетнем ряду колеблются. Колеблется вместе с ними и годовой объем стока. Эти колебания определяются столь большим числом факторов, что причинный анализ их практически неосуществим. Поэтому мы вынуждены рассматривать сток как случайный процесс, а характерные расходы воды – максимальный, минимальный, среднегодовой, – как случайные величины.

Поведение случайных величин описывается средствами математической статистики. Основным из этих средств служат функции распределения вероятностей. Так как функции распределения применяются в гидрологии к ряду случайных величин, то сведения о них дадим в общем виде.

Обозначим случайную величину X. Мы называем ее случайной потому, что она, по неизвестным нам конкретным причинам, может принимать неупорядоченные численные значения. В самом общем случае она может быть равна любому действительному числу 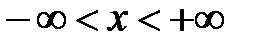. С точки зрения теории вероятностей, поведение величины X будет полностью определено, если для каждого числа х будет известна вероятность Р того, что 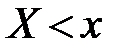. Функция решающая такую задачу, называется интегральной функцией распределения вероятностей.

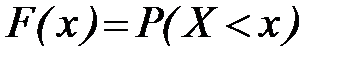. (9)

Вероятность Р называют вероятностью не превышения. При х= – ¥ функция F равна 0, при 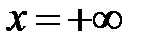она равна 1. Между этими пределами функция F монотонно возрастает вместе с x. Если случайная величина X может принимать только определенные дискретные значения (например, 0, 1, 2, ...), функция F терпит при этих значениях разрывы и изображается ступенчатой линией. Если, как это наблюдается с характерными расходами воды, случайная величина может принимать непрерывный набор значений, интегральная функция распределения также непрерывна. В этом случае от F(x) можно взять производную, получая в результате дифференциальную функцию распределения

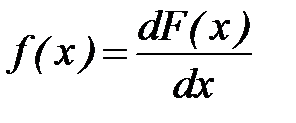(10)

Примерный вид интегральной и дифференциальной функций распределения показан на рис. 13. Дифференциал функции F(x) выражает вероятность того, что величина X принимает значения, лежащие между х и :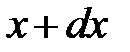

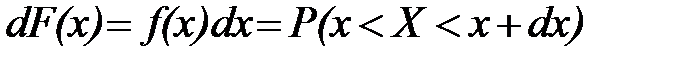. (11)

Очевидно, эта вероятность тем больше, чем больше f(x). В связи с этим функцию f(x) называют также функцией плотности распределения вероятностей. Интегральная функция распределения вероятностей выражается через дифференциальную функцию формулой

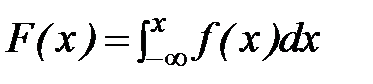(12)

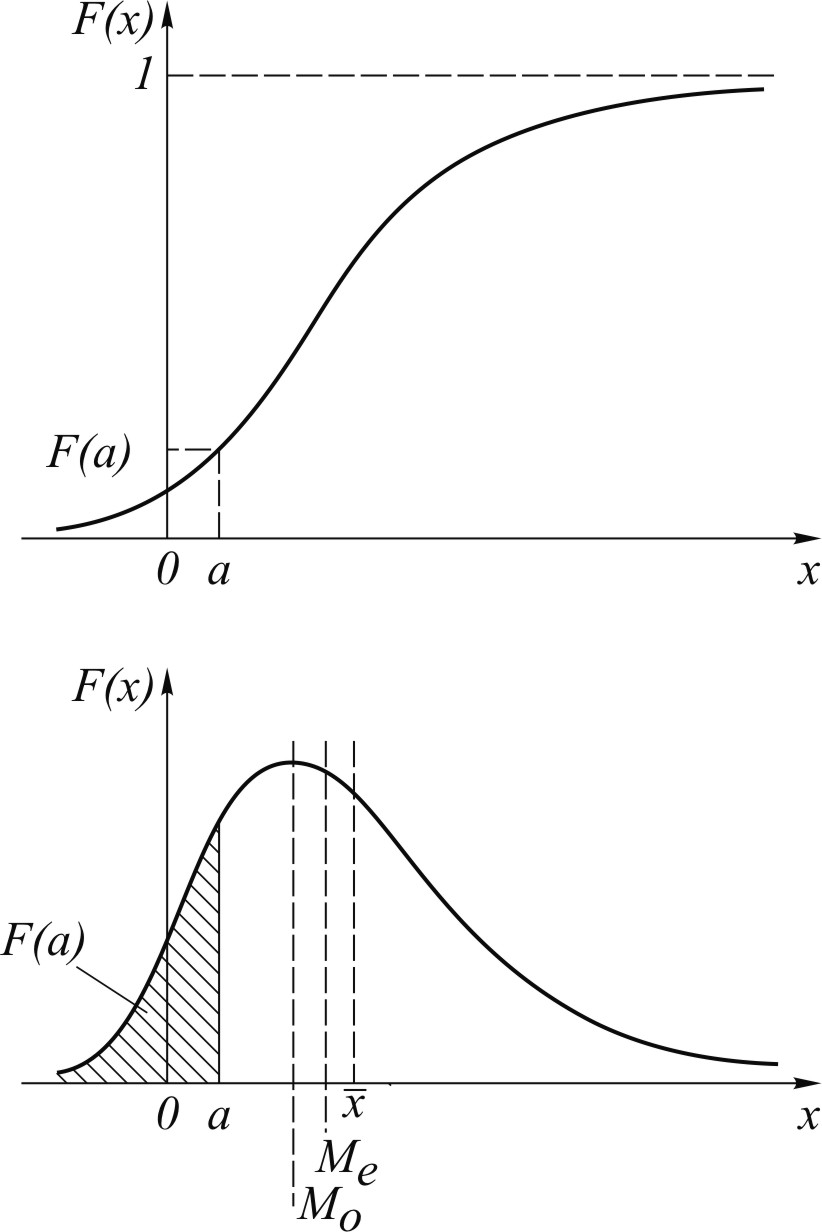Рис. 13. Графики: интегральной (а) и дифференциальной (б) функций распределения вероятности

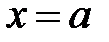Таким образом, вероятность не превышения величиной X некоторого заданного числа равна площади под графиком f(x), ограниченной справа перпендикуляром к оси х в точке 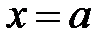(на рис. 13 эта площадь заштрихована). Подставив в верхнем пределе интеграла (12) значение 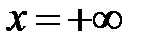, получим

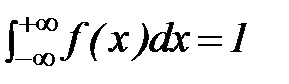, (13)

полная площадь под графиком f(x) равна единице.

Умножив текущую переменную х на дифференциал интегральной функции распределения 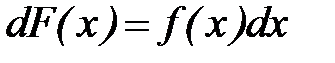, мы, тем самым, взвесим значения случайной величины X по их вероятностям и, проинтегрировав затем в пределах от
–¥ до + ¥, получим среднее значение X. Такое среднее называется
в теории вероятностей математическим ожиданием случайной величины X и обозначается

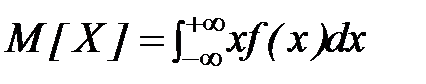. (14)

Для простоты записей будем обозначать математическое ожидание также через .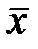

Если числа х получаются путем измерений и составляют дискретный ряд, то согласно закону больших чисел теории вероятности, с ростом числа измерений среднее арифметическое х_ср из измеренных х будет приближаться к математическому ожиданию величины X. Однако процесс такого приближения отличается от математического процесса стремления к пределу. Прибавив к большому числу измерений еще несколько, мы не обязательно улучшим значение х_ср (добавочные измерения могут все случайно отклониться от математического ожидания в одну сторону). В процессе приближения x_ср к 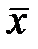разность 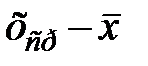испытывает случайные, постепенно затухающие колебания.

Математическое ожидание, которое называют также центром распределения, служит основным указанием положения, занимаемого случайной величиной на оси х. Добавочными характеристиками этого положения служат мода и медиана распределения. Модой называется значение переменной х, отвечающее максимуму плотности распределения вероятностей. Медиана есть то значение х, которое делит площадь под графиком f(x) на две равные части (см. рис. 13). Обозначая медиану Me, имеем

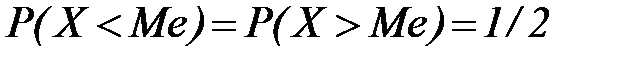. (15)

Дальнейшие сведения о свойствах распределения вероятностей величины X можно получить, используя моменты этой величины. Различают начальные и центральные моменты. Начальным моментом k-го порядка случайной величины X называется математическое ожидание k-й степени этой величины

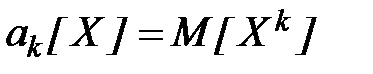. (16)

Начальный момент первого порядка есть, очевидно, не что иное, как математическое ожидание X. Центральным моментом k-го порядка случайной величины X называется математическое ожидание k-й степени отклонений этой величины от ее математического ожидания:

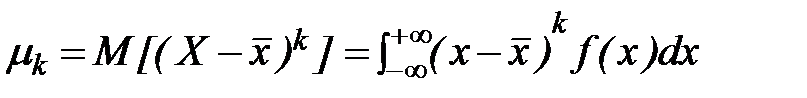. (17)

Первый центральный момент, очевидно, равен нулю. Второй цен тральный момент носит название дисперсии случайной величины:

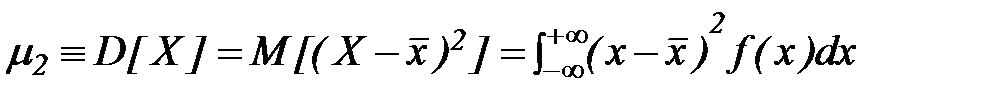. (18)

Корень квадратный из дисперсии называется средним квадратичным отклонением, или стандартом случайной величины X,

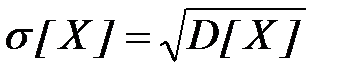. (19)

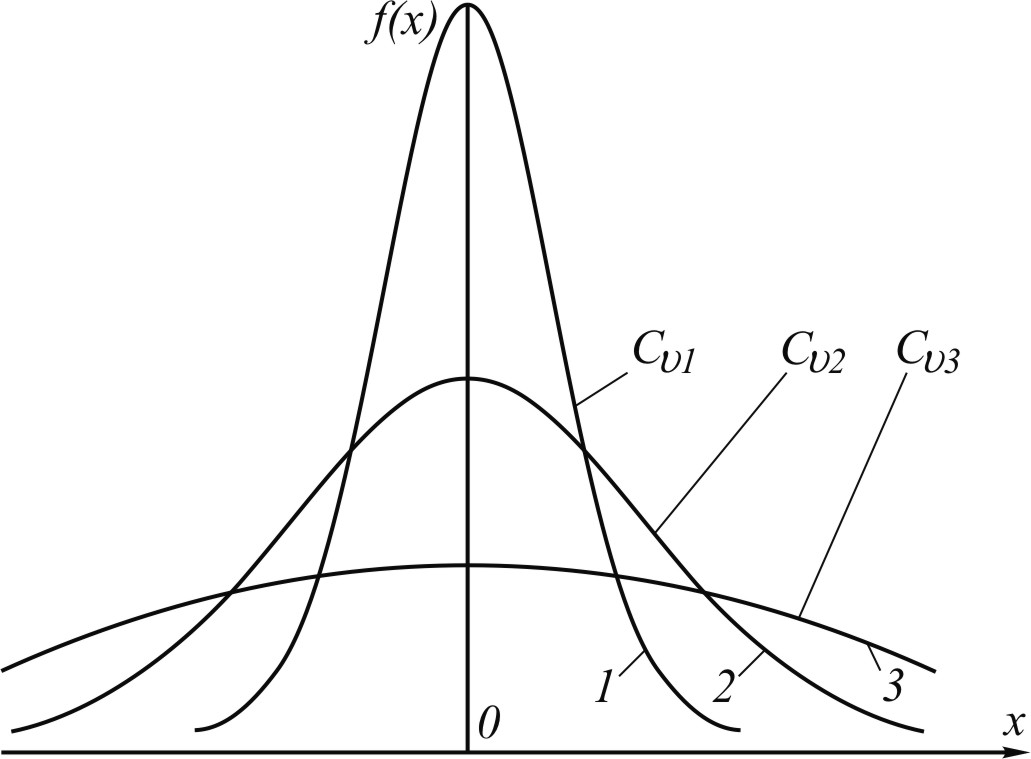Рис. 14. Графики дифференциальных функций распределения с разными значениями коэффициента вариации

Дисперсия и стандарт характеризуют рассеяние случайных значений X – степень разброса этих значений относительно центра распределения. Разделив стандарт на математическое ожидание X, получим безразмерную характеристику рассеяния, называемую коэффициентом вариации случайной величины

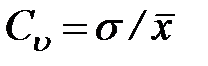. (20)

На рис. 14 показаны графики дифференциальных функций распределения с разными значениями коэффициента вариации. Как известно, площадь под каждой из этих кривых одна и та же – она равна единице. Чем больше коэффициент вариации, тем ниже максимум f(x), тем более распластанный характер имеет график функции.

Показанные на рис. 14 графики симметричны относительно центра распределения – равные по абсолютной величине положительные и отрицательные отклонения величины X от ее математического ожидания имеют одну и ту же плотность распределения. Математическое ожидание, мода и медиана у таких функций распределения совпадают. Иначе выглядит дифференциальная функция распределения, представленная на рис. 13, б, – она асимметрична. Асимметрию функций распределения характеризует третий центральный момент:

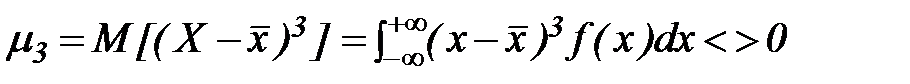. (21)

Разделив третий центральный момент на куб среднего квадратичного отклонения, получим безразмерную характеристику асимметрии распределения, называемую коэффициентом асимметрии.

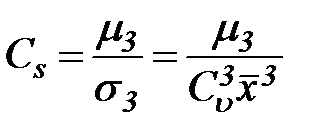. (22)

У симметричных функций распределения C_s=0. Наиболее важным и широко применяемым симметричным распределением является нормальное распределение с функцией плотности вида:

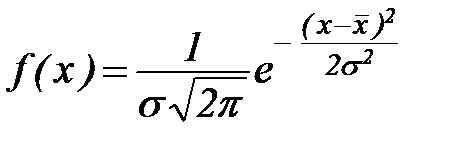. (23)

Нормальное распределение имеют случайные ошибки измерений.

Графики функций плотности распределения с положительным и отрицательным значениями C_s показаны на рис. 15. Функция плотности на рис. 13, б имеет положительную асимметрию. Как видно из рис. 13, б и рис. 15, при положительной асимметрии распределения вероятность положительных отклонений X от 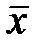меньше, чем отрицательных, но по абсолютной величине положительные отклонения превосходят отрицательные. Этим и объясняется, что математическое ожидание куба отклонений оказывается больше нуля. Для распределений с отрицательной асимметрией картина обратная.

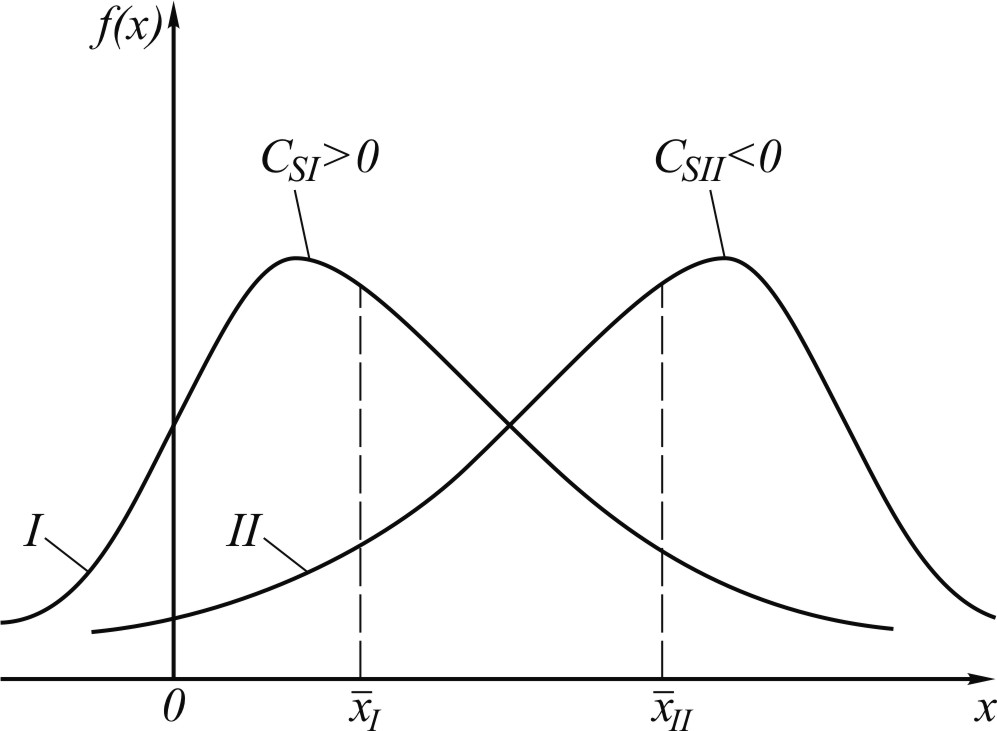Рис. 15. Графики дифференциальных функций распределения с положительной (I) и отрицательной (II) асимметрией

Математическое ожидание, коэффициент вариации и коэффициент асимметрии являются главными параметрами распределений случайных величин, включая и величины речного стока. В силу исторически сложившейся традиции в гидрологии вместо интегральных функций распределения обычно применяется их дополнение до единицы.

Функция:

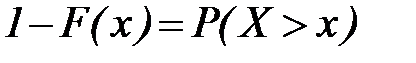(24)

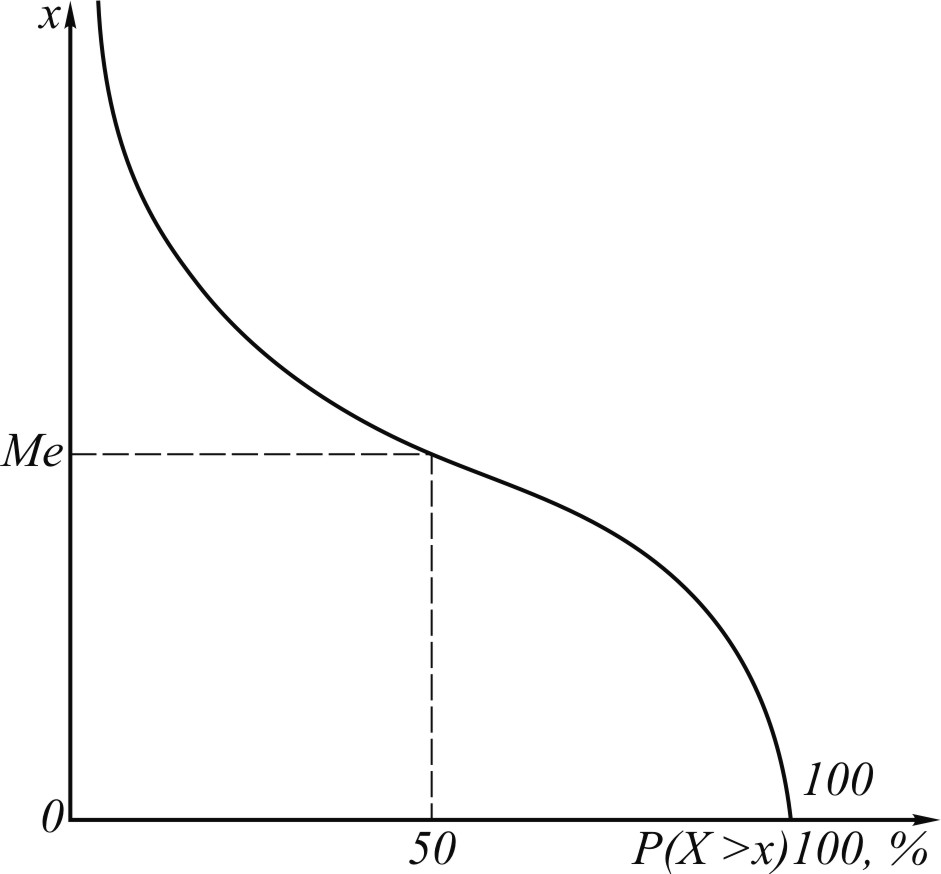Рис. 16. Кривая обеспеченности

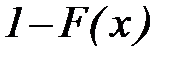называется функцией обеспеченности или надежности. Обеспеченность, таким образом, есть вероятность превышения случайной величиной X значений текущей переменной х. Опять таки по традиции при графическом изображении функции значения x (всегда большие нуля) откладываются по оси ординат, а значения 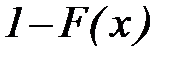– по оси абсцисс (рис. 16), причем они умножаются на 100, т.е. выражаются в процентах.

Норма стока

Как уже указывалось, норма стока – это средний за многолетие объем годового стока w₀. Равноправным выражением нормы стока служит средний многолетний расход воды 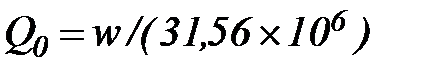. Норма стока может быть выражена также через средний годовой слой стока у₀ и средний многолетний модуль стока М₀. Здесь преимущественно будем пользоваться средним многолетним расходом воды. При наличии длительного ряда наблюдений он определяется как среднее арифметическое из наблюденных среднегодовых расходов:

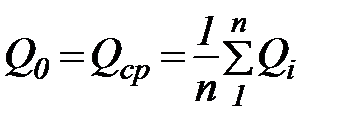, (25)

где: n – число лет наблюдений и i – порядковый номер года.

Если число лет устремить к бесконечности, то средний арифметический расход совпадает с математическим ожиданием годового расхода. Мы имели бы в этом случае «истинную» норму стока: Q₀=M[Q] (говоря так, мы, разумеется, отвлекаемся от реальной длительности климатических эпох, определяющих устойчивые режимы стока). Так как все ряды наблюдений ограничены, то совпадение среднего арифметического с математическим ожиданием может произойти лишь случайно, а в общем случае необходимо считаться с тем, что оно как-то отличается от математического ожидания. Приближенную величину среднего квадратичного отклонения среднего арифметического расхода Q_cp от математического ожидания можно найти по формуле

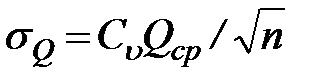. (26)

Таким образом, это отклонение или, иначе говоря, средняя квадратичная ошибка нормы стока тем больше, чем больше изменчивость годового стока и чем меньше число лет наблюдений. Относительную величину ошибки получим, разделив обе части равенства (26) на Q_ср.

Изменчивость годового стока зависит от физико-географических условий бассейна и более слабо – от его площади (увеличение площади сглаживает влияние местных колебаний стока). Наименьшая изменчивость годового стока наблюдается в зоне избыточного и достаточного увлажнения, где значения коэффициента вариации среднегодовых расходов обычно составляют 0,15-0,25. В лесостепной зоне СССР значения C_u увеличиваются до 0,3-0,6, а в степной – до 0,6-1,0. Воспользовавшись этими цифрами и формулой (26), можно найти, что для определения нормы стока с ошибкой не более 10% достаточно иметь ряды наблюдений: в северной части нашей страны 10 лет, в лесостепной зоне 35 и в степной 100 лет.

В тех случаях, когда длительность ряда недостаточна для определения нормы стока с требуемой точностью (5-10%), выход из затруднения дает использование бассейнов-аналогов. Желая определить норму стока в бассейне с малым n, ищут бассейн, близкий по своим климатическим условиям и факторам подстилающей поверхности к данному, но освещенный длительными наблюдениями над стоком. Далее по сведениям за годы параллельных наблюдений строят график связи между среднегодовыми расходами в двух створах. Обычно такой график получается линейным. Располагая графиком связи, восстанавливают среднегодовые расходы в створе с недостаточным числом лет наблюдений по расходам в замыкающем створе бассейна-аналога за все то время, когда наблюдения велись в последнем створе и не велись в первом.