Колебания годового стока
Наблюдения над годовым стоком показывают, что его случайные колебания имеют положительную асимметрию: годы с отрицательными отклонениями от нормы (маловодные) встречаются чаще, чем годы с положительными отклонениями (многоводные) и крайние положительные отклонения по своей абсолютной величине превосходят крайние отрицательные отклонения. Из значительного числа известных в теории вероятностей асимметричных функций распределения колебаниям годового стока достаточно хорошо удовлетворяет распределение, известное под названием распределения Пирсона III типа[2]. Оно обычно и применяется на практике. Кривая f(x) III типа Пирсона ограничена слева конечным значением х, а справа уходит в бесконечность, асимптотически приближаясь к оси х. Если наименьшее возможное значение случайной величины X неотрицательно, то между параметрами распределения III типа – коэффициентами вариации и асимметрии – существует соотношение
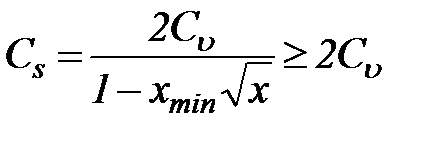 .
.
Указать наименьшее возможное значение годового стока в данном створе не представляется возможным. Так как отрицательного стока быть не может, то обычно условно полагают это наименьшее значение равным нулю, получая 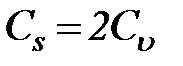 . Функция обеспеченности, отвечающая распределению III типа, табулирована и поэтому уравнения F(x) и f(x) не приводятся.
. Функция обеспеченности, отвечающая распределению III типа, табулирована и поэтому уравнения F(x) и f(x) не приводятся.
Чтобы воспользоваться теоретической таблицей обеспеченности, надо знать в интересующем нас створе норму стока и коэффициенты вариации и асимметрии. При наличии многолетнего ряда наблюдений, вычисление Cu и Cs ведется по формулам:
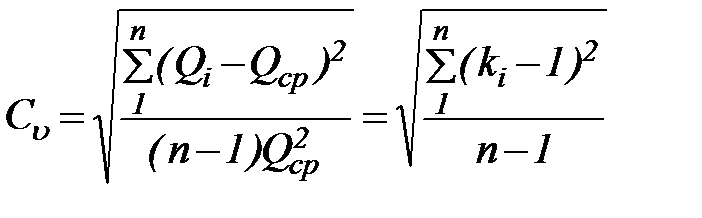 , (27)
, (27)
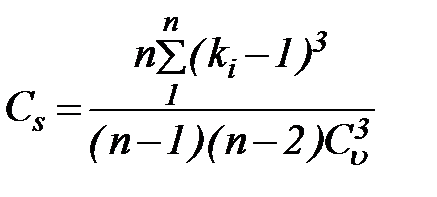 . (28)
. (28)
Безразмерные величины 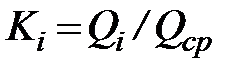 называются модульными коэффициентами.
называются модульными коэффициентами.
В формулах (27) и (28) подобно тому, как делается при вычислении нормы стока, математические ожидания квадрата и куба отклонений заменены соответствующими статистическими средними. Однако для получения этих средних сумма членов ряда делится не на число лет n, а на более сложные выражения: 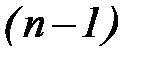 в формуле для Cv и
в формуле для Cv и 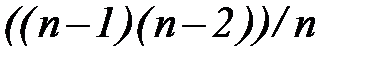 в формуле для Cs. Качественное объяснение такого способа вычисления средних состоит в следующем. Для самого грубого представления о норме стока достаточно одного года наблюдений. Для столь же грубого представления о дисперсии годового стока нужны по крайней мере два года. Чтобы иметь какую-то оценку асимметрии распределения, требуется не менее трех лет наблюдений. Иными словами, с повышением порядка момента некоторое число лет наблюдений как бы теряет ценность. Это и отражается способом подсчета средних. При n→¥ величины (n–1) и
в формуле для Cs. Качественное объяснение такого способа вычисления средних состоит в следующем. Для самого грубого представления о норме стока достаточно одного года наблюдений. Для столь же грубого представления о дисперсии годового стока нужны по крайней мере два года. Чтобы иметь какую-то оценку асимметрии распределения, требуется не менее трех лет наблюдений. Иными словами, с повышением порядка момента некоторое число лет наблюдений как бы теряет ценность. Это и отражается способом подсчета средних. При n→¥ величины (n–1) и 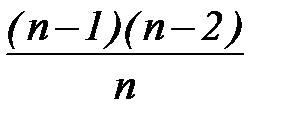 стремятся к n.
стремятся к n.
Обусловленная ограниченностью исходного стокового ряда относительная средняя квадратичная ошибка формулы (27) для коэффициента вариации, согласно указанию СН 435-72, может быть найдена по формуле
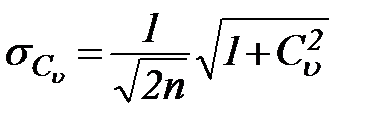 . (29)
. (29)
Относительную среднюю квадратичную ошибку формулы (28) для коэффициента асимметрии определяют по следующей формуле, полученной С.Н. Крицким и М.Ф. Менкелем в предположении Cs=2Cv
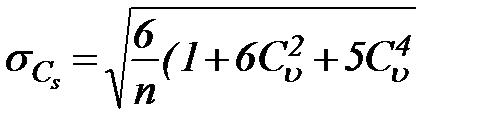 . (30)
. (30)
Таблица 3
Таблица Фостера-Рыбкина
| Сs | Относительные отклонения Ф модульных коэффициентов от единицы при различных P, % | |||||||||
| 0,01 | 0,1 | 1,0 | ||||||||
| 0.0 | 3.72 | 3.09 | 2.33 | 1.88 | 1.64 | 1.28 | 0.84 | 0.68 | 0.52 | 0.25 |
| 0.2 | 4.16 | 3.38 | 2.48 | 1.93 | 1.69 | 1.30 | 0.83 | 0.67 | 0.51 | 0.22 |
| 0.4 | 4.61 | 3.67 | 2.62 | 2.00 | 1.74 | 1.32 | 0.82 | 0.65 | 0.48 | 0.19 |
| 0.6 | 5.05 | 3.96 | 2.77 | 2.06 | 1.79 | 1.33 | 0.80 | 0.62 | 0.45 | 0.15 |
| 0.8 | 5.50 | 4.25 | 2.90 | 2.12 | 1.83 | 1.34 | 0.78 | 0.60 | 0.42 | 0.12 |
| 1.0 | 5.96 | 4.54 | 3.03 | 2.19 | 1.87 | 1.34 | 0.76 | 0.57 | 0.38 | 0.08 |
| 1.2 | 6.41 | 4.82 | 3.15 | 2.25 | 1.90 | 1.34 | 0.74 | 0.54 | 0.35 | 0.05 |
| 1.4 | 6.87 | 5.11 | 3.28 | 2.31 | 1.93 | 1.34 | 0.71 | 0.51 | 0.32 | 0.02 |
| 1.6 | 7.31 | 5.39 | 3.40 | 2.36 | 1.96 | 1.33 | 0.68 | 0.48 | 0.28 | -0.01 |
| 1.8 | 7.76 | 5.66 | 3.50 | 2.41 | 1.98 | 1.32 | 0.64 | 0.44 | 0.24 | -0.05 |
| 2.0 | 8.21 | 5.91 | 3.60 | 2.46 | 2.00 | 1.30 | 0.61 | 0.41 | 0.20 | -0.08 |
| Сs | 99,0 | 99,9 | ||||||||
| 0.0 | 0.00 | -0.25 | -0.52 | -0.68 | -0.84 | -1.28 | -1.64 | -1.88 | -2.33 | -3.09 |
| 0.2 | -0.03 | -0.28 | -0.55 | -0.70 | -0.85 | -1.25 | -1.58 | -1.79 | -2.18 | -2.81 |
| 0.4 | -0.06 | -0.31 | -0.57 | -0.71 | -0.85 | -1.22 | -1.51 | -1.69 | -2.03 | -2.54 |
| 0.6 | -0.09 | -0.34 | -0.58 | -0.72 | -0.86 | -1.19 | -1.45 | -1.59 | -1.88 | -2.28 |
| 0.8 | -0.13 | -0.37 | -0.60 | -0.73 | -0.86 | -1.16 | -1.38 | -1.49 | -1.74 | -2.03 |
| 1.0 | -0.16 | -0.40 | -0.61 | -0.73 | -0.86 | -1.12 | -1.31 | -1.39 | -1.59 | -1.80 |
| 1.2 | -0.19 | -0.42 | -0.62 | -0.73 | -0.85 | -1.08 | -1.25 | -1.30 | -1.45 | -1.59 |
| 1.4 | -0.22 | -0.44 | -0.63 | -0.73 | -0.84 | -1.05 | -1.18 | -1.21 | -1.32 | -1.40 |
| 1.6 | -0.25 | -0.46 | -0.64 | -0.73 | -0.82 | -1.00 | -1.11 | -1.13 | -1.19 | -1.24 |
| 1.8 | -0.28 | -0.48 | -0.64 | -0.72 | -0.80 | -0.95 | -1.03 | -1.06 | -1.08 | -1.11 |
| 2.0 | -0.30 | -0.49 | -0.64 | -0.71 | -0.78 | -0.90 | -0.95 | -0.98 | -0.99 | -1.00 |
Примечание: более полная таблица – до значений Сs = 5,2 имеется в «Руководстве по определению основных гидрологических характеристик» (Л., Гидрометеоиздат, 1973).
Согласно формуле (29) при 30-летнем периоде наблюдений ошибка в определении коэффициента вариации составляет 13-18%. Ошибку менее 10% можно ожидать лишь при рядах в 50-100 лет. Еще меньше точность определения Cs – даже при 100-летнем ряде наблюдений средняя квадратичная ошибка в величине Cs превышает 40%. Поэтому при практических расчетах обычно предпочитают находить Cs по соотношению 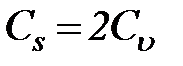 , проверяя согласие результата с наблюдениями путем наложения на теоретическую кривую обеспеченности точек эмпирической обеспеченности.
, проверяя согласие результата с наблюдениями путем наложения на теоретическую кривую обеспеченности точек эмпирической обеспеченности.
Таблица координат теоретической кривой обеспеченности, отвечающей распределению III типа Пирсона, была составлена А. Фостером и уточнена С.И. Рыбкиным (табл. 3). В таблице для ряда значений обеспеченности Р, %, и ряда значений коэффициента асимметрии Cs даны отклонения модульных коэффициентов от единицы, выраженные в долях коэффициента вариации:
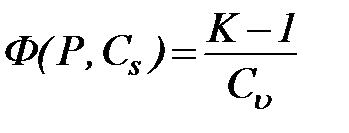 .
.
Таким образом, для получения ординат кривой обеспеченности среднегодовых расходов воды при известных Q0, Cu и Cs надо взять значения функции Ф из строчки таблицы, отвечающей данному Cs, и затем последовательно выполнить три операции: умножить значения Ф на Cu, прибавить к каждому из этих произведений единицу и результаты умножить на Q0:
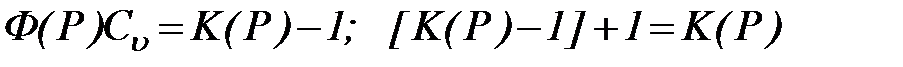 ;
;
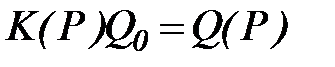 .
.
Таблица Фостера-Рыбкина наглядно демонстрирует мощь метода функций распределения. С ее помощью мы имеем возможность узнать (разумеется, приближенно) значения годового стока очень редкой повторяемости, например среднегодовой расход в маловодный год, встречающийся в среднем один раз в 1000 лет (Р = 99,9%).
Для построения эмпирической кривой обеспеченности наблюденные за n лет средние годовые расходы располагают в убывающем порядке, а отвечающие им абсциссы подсчитывают по формуле
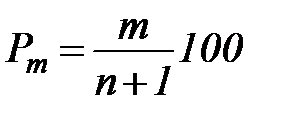 , (31)
, (31)
где: m – порядковый номер расхода в убывающем ряду.
Единица прибавляется в знаменателе к числу n для того, чтобы учесть ограниченность ряда наблюдений. Без этого при 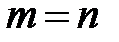 мы имели бы
мы имели бы 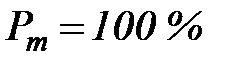 , что, очевидно, неверно. При
, что, очевидно, неверно. При 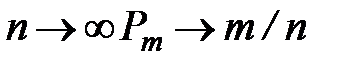 , а эта последняя величина, согласно закону больших чисел, приближается к теоретической обеспеченности.
, а эта последняя величина, согласно закону больших чисел, приближается к теоретической обеспеченности.
Наложение точек эмпирической обеспеченности на теоретическую кривую удобно делать на клетчатке вероятностей Хазена. Так называется расчетная бумага с равномерной числовой шкалой на оси у и со шкалой на оси х, разбитой таким образом, чтобы график обеспеченности, отвечающий нормальному закону (23), имел вид прямой линии. Кривизна графика обеспеченности, построенного на такой клетчатке, свидетельствует об асимметрии распределения. Обычно, положив Cs=2Cu, удается получить хорошее согласие между теоретической кривой обеспеченности и эмпирическими точками. Пример такого согласия показан на рис. 18. Если согласие недостаточное, то можно его улучшить, подобрав новое значение Cs>2Cu, однако прибегать к этому допустимо, лишь располагая большим числом эмпирических точек.
Если в интересующем нас створе число лет наблюдений недостаточно для надежного определения коэффициента вариации, прибегают к помощи бассейна-аналога. Есть несколько способов использования данных по бассейну-аналогу. Наиболее простой состоит в следующем. За n лет параллельных наблюдений вычисляют значения коэффициента вариации Cuna по бассейну-аналогу и Cun по бассейну с недостатком наблюдений. Зная коэффициент вариации CuNa по бассейну-аналогу за многолетний период наблюдений, находят расчетное значение коэффициента вариации в интересующем нас створе по формуле
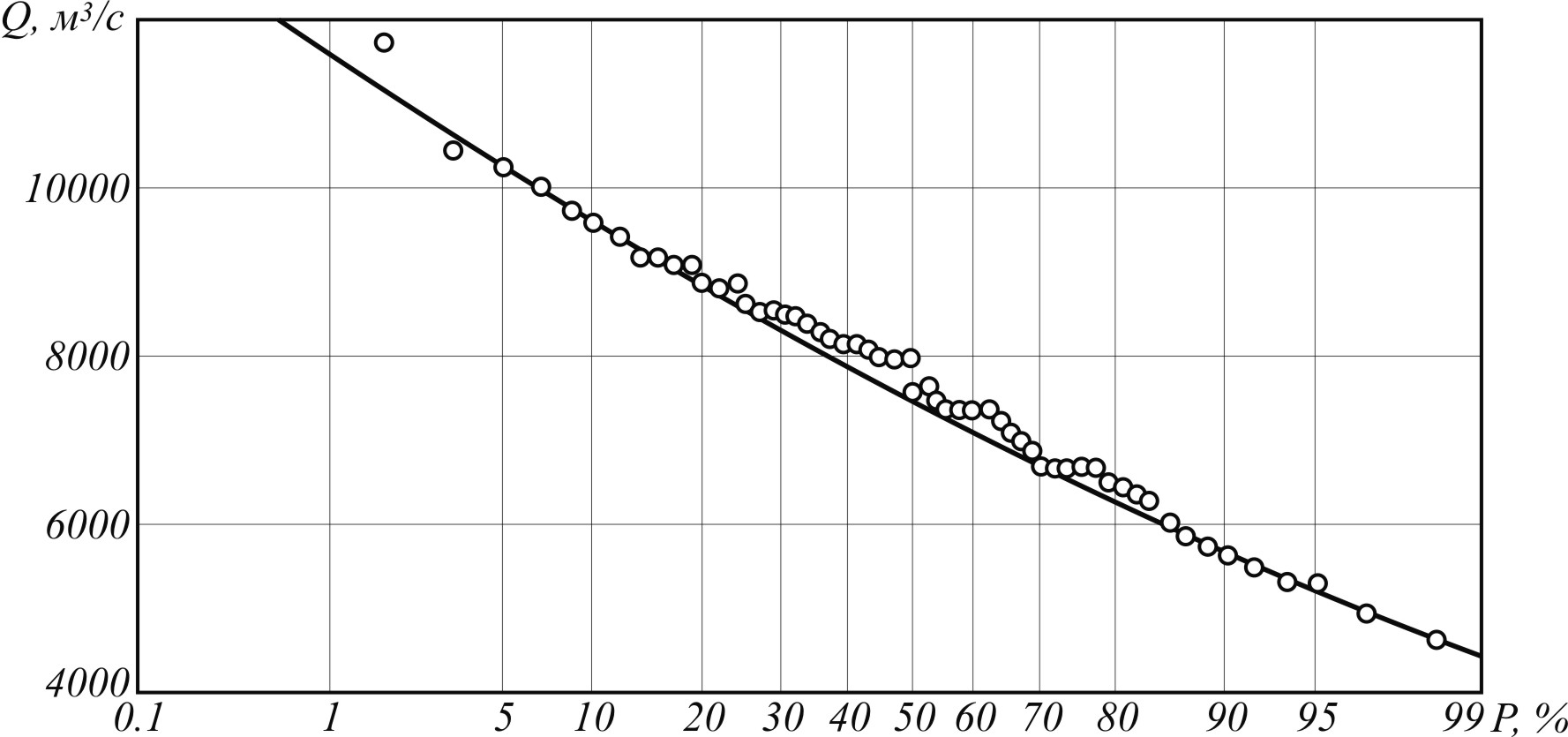 Рис.18. Кривая обеспеченности среднегодовых расходов воды
р. Волги у г. Cu=0.19; Cs=2Cu
Рис.18. Кривая обеспеченности среднегодовых расходов воды
р. Волги у г. Cu=0.19; Cs=2Cu
|
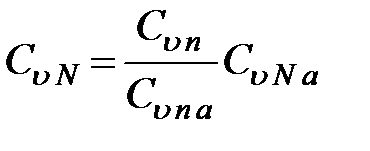 .
.
В тех случаях, когда наблюдений в данном створе нет совсем, величину Cu определяют или по карте изолиний коэффициента вариации, приведенной в СН 435-72, или по эмпирическим формулам.
Принципиальное преимущество формул состоит в том, что в них имеется возможность учесть влияние на коэффициент вариации не только физико-географических факторов, но также и площади бассейна. О том, что сток с малых водосборов изменчивее стока в больших, уже упоминалось при обсуждении точности определения нормы стока. Приведем формулу Д.Л. Соколовского:
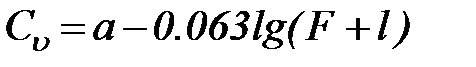 ,(32)
,(32)
где: F – площадь бассейна, км2;
a – параметр, для которого имеется карта изолиний.
М.Э. Шевелев нашел, что параметр а можно выразить в виде функции среднего модуля стока:
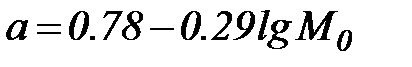 .(33)
.(33)
На ETC параметр а возрастает с севера на юг и юго-восток в пределах от 0,5 до 0,9.
Для работы водохранилищ важное значение имеет вопрос о цикличности колебаний годового стока. Положительная асимметрия колебаний стока, увеличивая число маловодных лет по сравнению с числом многоводных, делает группировки из нескольких маловодных лет подряд более вероятными, чем такие же группировки многоводных лет. Наблюдения подтверждают этот вывод. На протяжении текущего столетия на реках ETC наблюдались два резко маловодных периода – 1919-1921 гг. и 1935-1939 гг., причем последний, охвативший весь бассейн Волги, привел к не восполненному до сих пор снижению уровня Каспийского моря. Подобных группировок многоводных лет не наблюдалось. Д.Я. Раткович, исследовавший 371 ряд 40-летних наблюдений над стоком на 289 реках земного шара, нашел среди этого массива данных 433-летних комбинации маловодных лет со стоком обеспеченностью 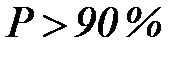 и 283-летних комбинаций многоводных лет со стоком обеспеченностью
и 283-летних комбинаций многоводных лет со стоком обеспеченностью 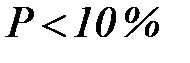 . Число резко маловодных трехлетий оказалось, таким образом, в 1,5 раза больше числа резко многоводных трехлетий. Причину этой особенности многолетних колебаний стока, а с ней и причину самой положительной асимметрии колебаний, по-видимому, следует видеть в том, что между среднегодовыми расходами смежных маловодных лет существует несколько более тесная стохастическая связь, чем между среднегодовыми расходами смежных многоводных лет (наличие корреляции – довольно слабой – между стоками смежных лет установлено как общий факт уже давно). Речному бассейну труднее вернуться к норме после маловодного года, чем после многоводного.
. Число резко маловодных трехлетий оказалось, таким образом, в 1,5 раза больше числа резко многоводных трехлетий. Причину этой особенности многолетних колебаний стока, а с ней и причину самой положительной асимметрии колебаний, по-видимому, следует видеть в том, что между среднегодовыми расходами смежных маловодных лет существует несколько более тесная стохастическая связь, чем между среднегодовыми расходами смежных многоводных лет (наличие корреляции – довольно слабой – между стоками смежных лет установлено как общий факт уже давно). Речному бассейну труднее вернуться к норме после маловодного года, чем после многоводного.
Дефицит стока, который создается в результате наступления нескольких маловодных лет подряд, определяет объем водохранилища, нужный для многолетнего регулирования стока
Дата добавления: 2017-04-05; просмотров: 2722;











