Другие важные экстремальные задачи на графах

Кратчайшие пути

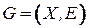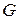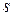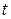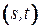Пусть ‑ ориентированный взвешенный граф. Задача о кратчайшем пути [6] состоит в отыскании пути минимального веса, соединяющего заданные начальную и конечную вершины графа при условии, что хотя бы один такой путь существует. Начальную и конечную вершины обозначим соответственно через и ; -путь минимального веса будем называть кратчайшим 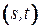-путем.

Вначале рассмотрим случай, когда веса всех дуг графа неотрицательны, т. е. 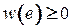для каждой дуги .

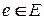В этом случае решение задачи о кратчайшем пути является существенно менее трудоемким, чем в общем случае. Первый эффективный алгоритм построения кратчайшего пути в графе с неотрицательными весами дуг предложил Е. Дийкстра в 1959 г.

На каждой итерации этого алгоритма всякая вершина 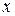графа 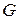получает метку 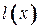, которая может быть постоянной либо временной. В первом случае 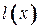вес кратчайшего 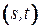-пути. Если же метка 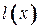временная, то 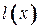‑ вес кратчайшего 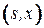-пути, проходящего только через вершины с постоянными метками. Таким образом, временная метка 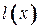является оценкой сверху для веса кратчайшего 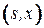-пути, и став на некоторой итерации постоянной, она остается такой до конца работы алгоритма. Кроме 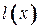, с каждой вершиной 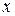графа 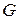, за исключением 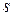, связывается еще одна метка ‑ 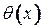. На каждой итерации 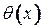является номером вершины, предшествующей 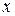в 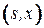-пути, имеющем минимальный вес среди всех 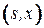-путей, проходящих через вершины, получившие к данному моменту постоянные метки. После того как вершина 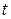получила постоянную метку, с помощью меток 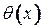легко указать последовательность вершин, составляющих кратчайший 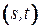-путь.

Перед началом первой итерации алгоритма вершина 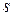имеет постоянную метку 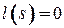, а метки 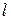всех остальных вершин равны 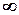и эти метки временные. Общая итерация алгоритма состоит в следующем. Пусть 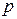‑ вершина, получившая постоянную метку 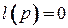на предыдущей итерации. Просматриваем все вершины 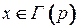, имеющие временные метки, с целью уменьшения (если это возможно) этих меток. Метка 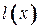вершины 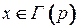заменяется на 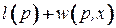, если оказалось, что 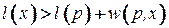. в этом случае говорим, что вершина 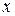получила свою метку 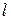из вершины 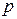, и полагаем 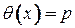. Если же 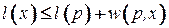, то метк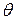и и 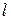вершины 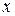не изменяются на данной итерации. Алгоритм заканчивает работу, когда метка 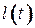становится постоянной. Как уже говорилось выше, 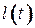‑ вес кратчайшего 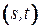-пути, который будем обозначать через 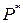. Этот путь определяется с помощью мето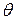к так:

,

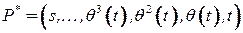где 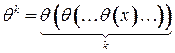для любой вершины .

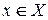[1] Заметим, что в определении отсутствует случай, когда в вершине 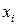имеется петля. Часто используется дополнительное значение для 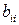(например, какой-нибудь символ или выражение «1 и -1»).

[2] Более общим по сравнению с ХГ является класс совершенных графов [34]. Граф 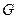называется со­вершенным, если для каждого порожденного гра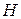фа графа 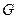выполняется равенство 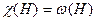. Задачи поиска таких графовых параметров, как 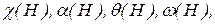для совершенных графов являются полиномиальными (т.е. разреши­мыми за полиномиальное время).

[3] Правда, этот метод столь же неэффективен, как и другие методы установления изоморфизма двух произвольных графов.

[4] Иногда нумерация понимается в более широком смысле. Это либо векторная нумерация , т.е. отображение вида 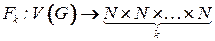(), либо отображение множества вершин в некоторое множество объектов нечисловой природы, например в множество символов некоторого алфавита, множество слов и т. д.

[5] Название «поиск в глубину» (в англоязычной литературе ‑ depth first search (DFS)) связано с тем, что при выполнении обхода графа по этим правилам мы стремимся проникнуть в глубь графа так далеко, как это возможно, затем отступаем на шаг назад и снова стремимся пройти вперед и так далее.

[6] DFS = depth first search (поиск в глубину).

[7] Как известно, матрицы 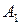и 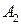, удовлетворяющие условию (4.3), называются подобными. Разработаны алгебраические методы, позволяющие решить вопрос о подобии матриц 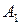и 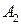. Представляется целесообразной попытка соединения алгебраических методов и описанных здесь подходов.

[8] Зыков А. А. Теория конечных графов. — Новосибирск: Наука, 1969.

[9] Appel K., Haken W. Every planar map is four colorable: Part I: Discharging // Illinois J. Math. ‑ 1977. ‑ 21. ‑ P. 429-490.

[10] Зыков А. А. Теория конечных графов. — Новосибирск: Наука, 1969.

[11] Так что с точки зрения сложности задача о минимальном остове действительно является легкой.